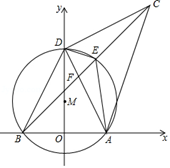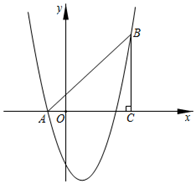
 B .
B . 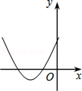 C .
C . 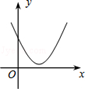 D .
D . 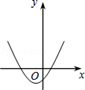
|
|
30≤t≤35 |
35<t≤40 |
40<t≤45 |
45<t≤50 |
合计 |
|
A |
59 |
151 |
166 |
124 |
500 |
|
B |
50 |
50 |
122 |
278 |
500 |
|
C |
45 |
265 |
167 |
23 |
500 |
早高峰期间,乘坐(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
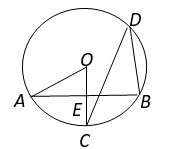
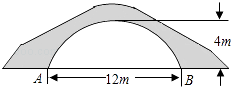
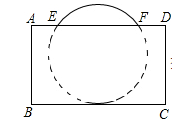
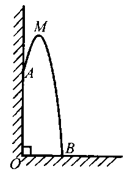
①抛物线型;②圆弧型. 已知这座桥的跨度L=32米,拱高h=8米.

|
销售单价(元) |
x+40 |
|
销售量y(件) |
|
|
销售玩具获得利润w(元) |
|