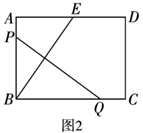
C .
C .  D .
D . 
a.四张卡片(形状、大小和质地都相同),正面分别写有“创建”“为民”“创建”“惠民”;
b.将这四张卡片背面朝上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张;
c.若抽取的两张卡片能组成“创建为民”或“创建惠民”,则获得一次成为“文明倡导者”的机会.
|
时间t/天 |
1 |
3 |
10 |
20 |
|
日销售量m/件 |
98 |
94 |
80 |
60 |
这20天中,该产品每天的价格y(单位:元/件)与时间t的函数关系式为: (t为整数),根据以上提供的条件解决下列问题: