2021-2022学年人教版九年级上册第二十三章旋转单元测...

更新时间：2021-07-02 浏览次数：269 类型：单元试卷

一、单选题

1. (2021八下·北仑期中) 下列图形中，既是轴对称图形又是中心对称图形的有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
2. (2023九下·盐都月考) 利用图形的旋转可以设计出许多美丽的图案．如图2中的图案是由图1所示的基本图案以点 $\text{[math]}$ 为旋转中心，顺时针（或逆时针）旋转角度 $\text{[math]}$ ，依次旋转五次而组成，则旋转角 $\text{[math]}$ 的值不可能是（）

A . 36° B . 72° C . 144° D . 216°

答案解析收藏纠错 + 选题
3. (2019·贵港) 若点P（m﹣1，5）与点Q（3，2﹣n）关于原点成中心对称，则m+n的值是（）

A . 1 B . 3 C . 5 D . 7

答案解析收藏纠错 + 选题
4. (2024九上·潮南期末) 如图，将△OAB绕点O逆时针旋转80°，得到△OCD.若∠A＝2∠D＝100°，则∠α的度数是（）

A . 50° B . 60° C . 40° D . 30°

答案解析收藏纠错 + 选题
5. (2021·泰州模拟) 始于唐代的青花瓷给人以古朴、典雅之美.关于如图所示的青花瓷图案，下列说法正确的是（）

A . 它是中心对称图形，但不是轴对称图形 B . 它是轴对称图形，但不是中心对称图形 C . 它既是中心对称图形，又是轴对称图形 D . 它既不是中心对称图形，又不是轴对称图形

答案解析收藏纠错 + 选题
6. (2019九下·昆明期中) 如图， $\text{[math]}$ 方格纸上的两条对称轴 $\text{[math]}$ 、 $\text{[math]}$ 相交于中心点 $\text{[math]}$ ，对△ABC分别作下列变换：
①先以点 $\text{[math]}$ 为中心顺时针方向旋转 $\text{[math]}$ ，再向右平移 $\text{[math]}$ 格、向上平移 $\text{[math]}$ 格；②先以点 $\text{[math]}$ 为中心作中心对称图形，再以点 $\text{[math]}$ 的对应点为中心逆时针方向旋转 $\text{[math]}$ ；③先以直线 $\text{[math]}$ 为轴作轴对称图形，再向上平移 $\text{[math]}$ 格，再以点 $\text{[math]}$ 的对应点为中心顺时针方向旋转 $\text{[math]}$ .其中，能将△ABC变换成△PQR的是（）

A . ①② B . ①③ C . ②③ D . ①②③

答案解析收藏纠错 + 选题
7. 已知点（a，a），给出下列变换：
①关于x轴的轴对称变换； ②关于直线y=﹣x的轴对称变换； ③关于原点的中心对称变换；④绕原点旋转180°．其中通过变换能得到像的坐标为（﹣a，﹣a）的变换是（　　）

A . ①②④ B . ②③④ C . ③④ D . ②③

答案解析收藏纠错 + 选题
8. (2021·南阳模拟) 在平面直角坐标系中，已知点P（x₀ ， ﹣y₀），连接OP，将线段OP绕点O顺时针旋转90°后，得到线段OQ，则点Q的坐标是（）

A . （﹣y₀ ， ﹣x₀） B . （﹣y₀ ， x₀） C . （y₀ ， x₀） D . （﹣x₀ ， y₀）

答案解析收藏纠错 + 选题
9. (2020八下·成都期中) 如图，已知正方形ABCD的边长为3，E为CD上一点，DE=1，以点A为中心，把△ADE顺时针旋转90°得△ABE'，连接EE'，则EE'的长度为（）

A . $\text{[math]}$ B . 4 C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2020九上·椒江月考) 如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形OA₁B₁C₁ ，依此方式，绕点O连续旋转2020次得到正方形OA₂₀₂₀B₂₀₂₀C₂₀₂₀ ，如果点A的坐标为（1，0），那么点B₂₀₂₀的坐标为（）

A . （﹣1，1） B . (- $\text{[math]}$ ，0) C . （﹣1，﹣1） D . (0，- $\text{[math]}$ )

答案解析收藏纠错 + 选题

二、填空题

11. (2020·九江模拟) 在 ①平行四边形、 ②正方形、 ③等边三角形、 ④等腰梯形、 ⑤菱形、 ⑥圆、⑦正八边形这些图形中，既是轴对称图形又是中心对称图形的是（填序号）

答案解析收藏纠错 + 选题
12. (2020九上·佳木斯期中) 若点（a+1,3）与点（-2，b-2）关于y轴对称，则点P（-a,b）关于原点对称的点的坐标为

答案解析收藏纠错 + 选题
13. (2020·澧县模拟) 如图，在△ABC中，AC=BC，将△ABC绕点A逆时针旋转60°，得到△ADE.若AB=2，∠ACB=30°，则线段CD的长度为.

答案解析收藏纠错 + 选题
14. (2021九上·南雄期中) 如图，在6×4方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是．

答案解析收藏纠错 + 选题
15. (2020八下·高港期中) 如图，△ABC中，∠ACB=90°，∠ABC=32°，以点C为旋转中心顺时针旋转后得到△A′B′C，且点A在边A′B′上，则旋转角的度数为．

答案解析收藏纠错 + 选题
16. (2020九上·金昌期中) 如图，将一个顶角为30°角的等腰△ABC绕点A顺时针旋转一个角度α（0＜α＜180°）得到△AB'C′，使得点B′、A、C在同一条直线上，则α等于°．

答案解析收藏纠错 + 选题
17. (2019八下·潍城期末) 如图，在直角坐标系中，已知点A（﹣3，0），B（0，4），对△OAB连续作旋转变换，依次得到△₁、△₂、△₃、△₄…，则△₂₀₂₀的直角顶点的坐标为．

答案解析收藏纠错 + 选题
18. (2018八上·云南期末) 如图，四边形ABCD为长方形， $\text{[math]}$ 旋转后能与 $\text{[math]}$ 重合，旋转中心是点；旋转了多少度；连结FC，则 $\text{[math]}$ 是三角形．

答案解析收藏纠错 + 选题

三、解答题

19. (2019九上·东莞期中) 已知点P(2x，y²+4)与Q(x²+1，-4y)关于原点对称，求x+y的值。

答案解析收藏纠错 + 选题
20. (2019八下·驿城期末) 如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（-3，1），B（-1，3），C（0，1）.

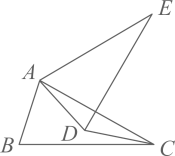
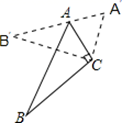
（ 1 ）将△ABC以点C为旋转中心旋转180°，画出旋转后的△A₁B₁C；

（ 2 ）平移△ABC，若点A的对应点A₂的坐标为（-5，-3），画出平移后的△A₂B₂C₂；

（ 3 ）若△A₂B₂C₂和△A₁B₁C关于点P中心对称，请直接写出旋转中心P的坐标.

答案解析收藏纠错 + 选题
21. (2017·延边模拟) 如图所示，网格中每个小正方形的边长为1，请你认真观察图（1）中的三个网格中阴影部分构成的图案，解答下列问题：
1. （1）这三个图案都具有以下共同特征：都是对称图形，都不是对称图形．
2. （2）请在图（2）中设计出一个面积为4，且具备上述特征的图案，要求所画图案不能与图（1）中所给出的图案相同．
答案解析收藏纠错 + 选题
22. (2021九上·和平期末) 如图，若在正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 为 $\text{[math]}$ 边上一点，点 $\text{[math]}$ 为 $\text{[math]}$ 延长线上一点，且 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 之间有怎样的数量关系和位置关系？请说明理由.

答案解析收藏纠错 + 选题
23.
如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（3，2）、B（3，5）、C（1，2）．
1. （1）在平面直角坐标系中画出△ABC关于x轴对称的△A₁B₁C_1；
2. （2）把△ABC绕点A顺时针旋转一定的角度，得图中的△AB₂C₂ ，点C₂在AB上．
  ①旋转角为多少度？
  ②写出点B₂的坐标．
答案解析收藏纠错 + 选题
24. (2019九上·思明期中) 已知Rt△ABC中，∠ACB＝90°，CA＝CB＝4，另有一块等腰直角三角板的直角顶点放在C处，CP＝CQ＝2，将三角板CPQ绕点C旋转（点P在△ABC内部），连接AP、BP、BQ ．
1. （1）求证：AP＝BQ；
2. （2）当PQ⊥BQ时，求AP的长．
答案解析收藏纠错 + 选题
25. (2018九上·南山期末) 如图，已知正方形ABCD，E是AB延长线上一点，F是DC延长线上一点，且满足BF=EF，将线段EF绕点F顺时针旋转90^。得FG，过点B作FG的平行线，交DA的延长线于点N，连接NG．
1. （1）求证：BE=2CF；
2. （2）试猜想四边形BFGN是什么特殊的四边形，并对你的猜想加以证明．
答案解析收藏纠错 + 选题