 B .
B .  C .
C .  D .
D . 


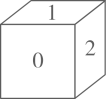
推理过程:因为和
互补,
所以 ▲ °.( ▲ ),
因为点O在直线AB上,所以 .
所以 ,
所以 . ( ▲ )
中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有这样一个问题:“今有三人共车,二车空;二人共车,九人步,问人和车各几何?”这个题的意思是:今有若干人乘车.若每3人乘一辆车,则余2辆空车;若每2人乘一辆车.则余9人需步行,问共有多少辆车,多少人?
某小组选择用一元一次方程解决问题,请补全他们的分析过程:
第一步,设共有x辆车;
第二步,由“若每3人乘一辆车,则余2辆空车”,可得人数为 ▲ (用含x的式子表示);
第三步,由“若每2人乘一辆车,则余9人需步行”.可得人数为 ▲ (用含x的式子表示);
第四步,根据两种乘车方式的人数相等,列出方程为 ▲ .

运输公司 | 起步价(单位:元) | 里程价(单位:元/千米) |
甲 | 1000 | 5 |
乙 | 500 | 10 |
例如:如图,点Q1 , Q2 , Q3在同一条直线上, Q1Q2=3,Q2Q3=6,则点Q1是点Q2到点Q3的 倍分点,点Q1是点Q3到点 Q2的3倍分点.
![]()
已知:在数轴上,点A,B,C分别表示-4,-2,2.
![]()