20.
(2022高一上·东城期末)
人口问题是世界普遍关注的问题,通过对若干个大城市的统计分析,针对人口密度分布进行模拟研究,发现人口密度与到城市中心的距离之间呈现负指数关系.指数模型

是经典的城市人口密度空间分布的模型之一,该模型的计算是基于圈层距离法获取距城市中心距离和人口密度数据的,具体而言就是以某市中心位置为圆心,以不同的距离为半径划分圈层,测量和分析不同圈层中的人口状况.其中x是圈层序号,将圈层序号是x的区域称为“x环”(

时,1环表示距离城市中心0~3公里的圈层;

时,2环表示距离城市中心3~6公里的圈层;以此类推);

是城市中心的人口密度(单位:万人/平方公里),

为x环的人口密度(单位:万人/平方公里);b为常数;

. 下表为某市2006年和2016年人口分布的相关数据:
年份 | 
| b |
2006 | 2.2 | 0.13 |
2016 | 2.3 | 0.10 |
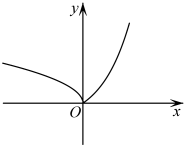 B .
B . 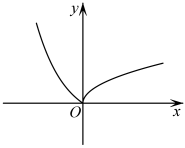 C .
C . 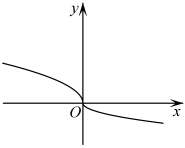 D .
D . 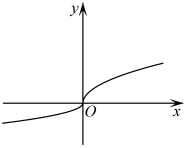
的图象关于点
对称;
的图象关于直线
对称.