一、选择题(本大题共8个小题,每小题4分,共32分.)
-
-
2.
(2024七上·梁平期末)
“数”读二十大报告,见证中国的非凡十年.十年来,全国832个贫困县全部摘帽,基本养老保险覆盖10.4亿人,国内生产总值从54万亿增长到114万亿元,居民人均可支配收入从16500元增加到35100元等.其中,数据35100用科学记数法表示应为( )
A . 0.351×105
B . 351×102
C . 3.51×104
D . 35.1×103
-
-
-
A .  与
与 B . -22与(-2)2
C . -(-3)与-|-3|
D . (-2)3与-23
B . -22与(-2)2
C . -(-3)与-|-3|
D . (-2)3与-23
-
A . a+c<0
B . b-a>0
C . ac>0
D . 
-
7.
(2022七上·武侯期中)
在下列说法中:①如果

,则有

;②0既不是正数,也不是负数;③一个有理数的绝对值是它本身,则这个数是正数;④若

,则m、n互为相反数.正确的个数有( )
A . 4个
B . 3个
C . 2个
D . 1个
-
8.
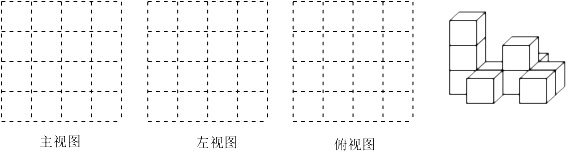
(2022七上·武侯期中)
如图,是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图,若组成这个几何体的小正方体的个数最多为m,最少为n,则m-n的值为( )

A . 4
B . 3
C . 2
D . 1
二、填空题(本大题共5个小题,每小题4分,共20分.)
三、解答题(共48分,答聚写在答题卡上)
-
-
(1)

;
-
(2)

;
-
(3)

;
-
(4)
-22-(-2)2-8÷(-2)3-42÷|-4|.
-
-
-
-
(2)
求

的值.
-
-
18.
(2022七上·武侯期中)
阅读理解:若A、B、C为数轴上三点,若点C到点A的距离是点C到点B的距离3倍,我们就称点C是【A,B】的金点.例如,如图1,点A表示的数为-1,点B表示的数为3.表示数2的点C到点A的距离是3,到点B的距离是1,那么点C是【A,B】的金点,但点C不是【B,A】的金点.

-
(1)
如图1,点B【D,C】的金点(填“是”或“不是”);点D是【,】的金点.
-
(2)
如图1,若点G是【A,C】的金点,则点G在数轴上表示的数是多少?
-
(3)
如图2,A、B为数轴上两点,点A所表示的数为-8,点B所表示的数为20.现有一点P从点B出发,向左运动,若点P运动到A点停止,点P在数轴上某处时,此时点P、A和B中恰有一个点为其余两点的金点,则点P表示的数是多少?(直接写出答案)
四、填空题(本大题共5个小题,每小题4分,共20分.)
-
19.
(2022七上·武侯期中)
已知a,b为有理数,且a>0,b<0,a+b<0,将四个数a,b,﹣a,﹣b按由大到小的顺序排列是
.(用“>”号连接)
-
-
21.
(2022七上·武侯期中)
如果规定符号“*”的意义是

, 比如3*1=3
2-1=8,2*3=3
2+2=11,求(-3)*(-2)+4
*(-1)=
.
-
22.
(2022七上·武侯期中)
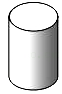
图中的大矩形长8厘米、宽6厘米,小矩形长4厘米、宽3厘米,以长边中点连线(图中的虚线)为轴,将图中的阴影部分旋转一周得到的几何体的表面积为
平方厘米.

-
23.
(2022七上·武侯期中)
我们常用的数是十进制的数,而计算机程序处理中使用的是只有数码0和1的二进制数.这两者可以相互换算,如将二进制数101换算成十进制数应为1×2
2+0×2
1+1×2
0=4+0+1=5,将1101换算成十进制数应为1×2
3+1×2
2+0×2
1+1×2
0=13,按此方式,则将十进制数25换算成二进制数应为
.
五、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)
-
24.
(2022七上·武侯期中)
小尚的妈妈在某玩具厂工作,厂里规定每周工作五天,该厂实行工资“日结算制”:每天的基本工资为200元,每天基本任务量为40个,若超额完成任务,则超出部分每个按7元奖励;若未完成任务,则未完成部分每个按8元扣除.由于种种原因,实际每天生产量与计划量相比有出入,本周五小尚妈妈刚好完成基本任务.下表是小尚妈妈本周的生产情况(比前一个工作日多记为正,比前一个工作日少记为负):
|
星期
|
一
|
二
|
三
|
四
|
五
|
|
增减产值
|
+5
|
-7
|
+1
|
+1
|
+4
|
-
(1)
根据记录的数据可知小尚妈妈星期三生产玩具个;本周实际生产玩具个;
-
-
(3)
若将工资“日结算制”改为“周结算制”,即每周的基本工资为1000元,每周基本任务为200个;若超额完成任务,则超出部分每个按7元奖励;若未完成任务,则未完成部分每个按8元扣除,在此方式下小尚妈妈本周的工资与“日结算制”的工资哪一个更多?请说明理由.
-
-
-
-
(3)
如果现在你还有一些棱长都为2cm的小正方体,要求保持俯视图和左视图都不变,最多可以再添加个小正方体.
-
26.
(2022七上·武侯期中)
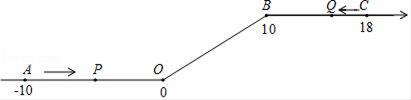
如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.问:
-
-
(2)
P、Q两点相遇时,求出相遇点M所对应的数是多少;
-
(3)
求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
 C .
C .  D .
D .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
![]()