一、选择题(本题有10小题,每小题4分,共40分,每小题只有一个选项是正确的,不选、多选、错选,均不给分)
-
A .  B .
B .  C . 2023
D . -2023
C . 2023
D . -2023
-
-
-
4.
在一个不透明的袋中装有9个只有颜色不同的球,其中2个白球、3个黄球和4个红球.从袋中任意摸出一个球,是黄球的概率为( )
-
-
-
-
8.
(2023九下·鹿城月考)
图1是一种落地晾衣架,晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,

和

分别是两根不同长度的支撑杆,其中两支脚

, 展开角

, 晾衣臂

, 则支樟杆的端点

离地面的高度

为( )
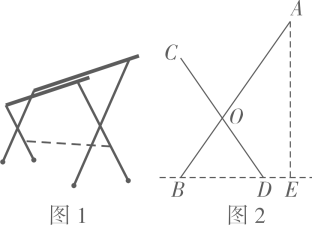
-
A . 若 , 函数有最大值5
B . 若
, 函数有最大值5
B . 若 , 函数有最小值5
C . 若
, 函数有最小值5
C . 若 , 函数有最小值1
D . 若
, 函数有最小值1
D . 若 , 函数无最大值
, 函数无最大值
-
10.
(2023九下·鹿城月考)
如图,在矩形

中,

, 延长

至点

, 使得

, 以

为直径的半圆

交

延长线于点

.欧几里得在《几何原本》中利用该图得到结论:矩形

的面积等于

的平方(即

).现连接

并延长交

于点

, 若

, 则

与矩形

的面积之比为( )
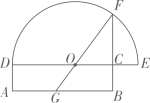
二、填空题(本题有6小题,每小题5分,共30分)
-
-
12.
(2023九下·鹿城月考)
甲、乙两名学生10次立定跳远成绩的平均数相同,若甲10次立定跳远成绩的方差为

, 乙10次立定跳远成绩的方差为

, 则甲、乙两名学生10次立定跳远成绩比较稳定的是
.(填“甲”或“乙”)
-
-
-
15.
(2023九下·鹿城月考)
如图,菱形

的边

在

轴,点

在第一象限,且

, 将这个菱形向右平移2个单位得到菱形

(点

和

对应).若反比例函数

的图象恰好经过点

, 则

的值为
.
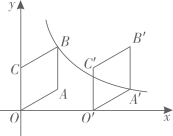
-
16.
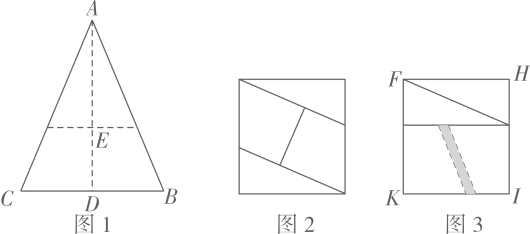
(2023九下·鹿城月考)
如图1,将一张等腰三角形纸片

沿虚线剪开,得到两个全等的三角形和两个全等的四边形小纸片.小博按图2方式拼接,恰好拼成一个不重叠、无缝隙的矩形;小雅按图3方式拼接,也拼出一个矩形

, 但由于两个四边形纸片有重叠(阴影)部分,整个面积减少了

.若

, 则

,矩形

的面积为

.
三、解答题(本题有8小题,共80分)
-
-
(1)
计算:

.
-
(2)
化简:

-
-
(1)
证明:

.
-
(2)
求

的度数.
-
-
(1)
在图1中画格点三角形

, 使其中一个内角为

.
-
(2)
在图2中画格点直角三角形

, 使

是其一边上的中线.
-
20.
(2023九下·鹿城月考)
今年体育中考后,某校王老师对本校同时报考篮球与排球的全体男学生的单项成绩进行了统计,数据整理如下:
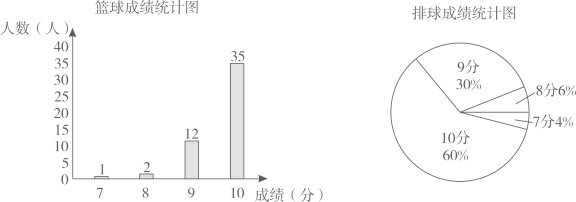
-
(1)
填写下表格.
|
项目
|
平均数(分)
|
众数(分)
|
中位数(分)
|
满分人数(个)
|
|
篮球
|
|
10
|
|
35
|
|
排球
|
|
10
|
10
|
|
-
(2)
结合学过的统计量,请你评价该校同时报考篮球与排球的全体男生的单项成绩,哪个项目成绩更好?
-
-
-
(2)
抛物线与

轴的另一交点为

, 将线段

向上平移

个单位,平移后的线段与抛物线分别交于点

(点

在点

左侧),若

, 求

的值.
-
22.
(2023九下·鹿城月考)
如图,在

中,

为

上一点,以

为直径的半圆

与

相切于点

, 与

相交于点

, 且

为

的中点,连结

, 过点

作

交

于点

.
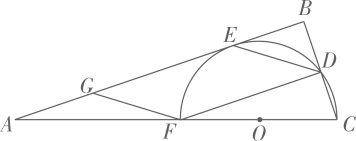
-
(1)
求证:四边

为平行四边形.
-
-
23.
(2023九下·鹿城月考)
根据以下素材,探索完成任务:
如何制定订餐方案? |
素材1 | 某班级组织春日研学活动,需提前为同学们订购午餐,现有A、B两种套餐可供选择,套餐信息及团购优惠方案如下所示: | 套餐类别 | 套餐单价 | 团体订购优惠方案 | | A:米饭套餐 | 30元 | 方案一:A套餐满20份及以上打9折;
方案二:B套餐满12份及以上打8折;
方案三:总费用满850元立减110元. | | B:面食套餐 | 25元 | | 温馨提示:方案三不可与方案一、方案二叠加使用. |
|
素材2 | 该班级共31位同学,每人都从A、B两种套餐中选择一种,一人一份订餐,拒绝浪费.经统计,有20人已经确定A或B套餐,其余11人两种套餐皆可.若已经确定套餐的20人先下单,三种团购优惠条件均不满足,费用合计为565元. |
问题解决 |
任务1 | 计算选择人数 | 已经确定套餐的20人中,分别有多少人选择A套餐和B套餐? |
任务2 | 分析变量关系 | 设两种套餐皆可的同学中有m人选择A套餐,该班订餐总费用为w元,当全班选择A套餐人数不少于20人时,请求出w与m之间的函数关系式. |
任务3 | 制定最优方案 | 要使得该班订餐总费用最低,则A、B套餐应各订多少份?并求出最低总费用. |
-
24.
(2023九下·鹿城月考)
如图,在四边形

中,

, 点

分别在边

和边

上,

.点

在

上从点

匀速运动到点

时,点

恰好从

上某一点匀速运动到点

, 记

, 已知

.
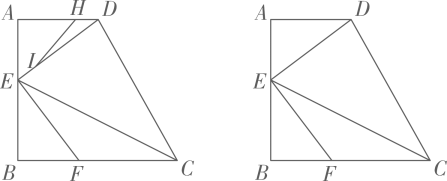
-
(1)
求证:

.
-
(2)
求

的长与

的值.
-
 B .
B .  C .
C .  D .
D . 




与
一边垂直时,求所有满足条件的
的值.
绕点
顺时针旋转
得到线段
, 当点
恰好落在
上时,求
和
的面积比.