云南省昭通市永善县2022-2023学年八年级下学期期末数学...

更新时间：2023-08-04 浏览次数：51 类型：期末考试

一、选择题(本大题共12小题，每小题只有一个正确选项，每小题3分，共36分)

1. (2023八下·永善期末) 中华文字是中国华夏民族5000年文化积淀的艺术现宝。下面4个汉字中，可以看作是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023八下·永善期末) 下列二次根式中能与 $\text{[math]}$ 合并的二次根式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023八下·永善期末) 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）

A . AB∥CD，AD∥BC B . AB=DC，AD=BC C . AO=CO，BO=DO D . AB∥DC，AD=BC

答案解析收藏纠错 + 选题
4. (2023八下·永善期末) 如图，在△ABC中，AC的垂直平分线交AB于点DCDC平分∠ACB，若 $\text{[math]}$ ，则∠B的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 35° D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八下·永善期末) 某射击运动员在训练中射击了10次，成绩如图所示：下列结论正确的是（）

A . 众数是8，中位数是8 B . 众数是8，中位数是8.5 C . 平均数是8.2，方差是1.2 D . 平均数是8.方差是1.2

答案解析收藏纠错 + 选题
6. (2023八下·永善期末) 如果点E、F、G、H分别是菱形ABCD四边AB、BC、CD、DA上的中点，那么四边形EFGH是（）

A . 菱形 B . 矩形 C . 正方形 D . 平行四边形

答案解析收藏纠错 + 选题
7. (2023八下·永善期末) 直线 $\text{[math]}$ 的图象如图所示，则函数 $\text{[math]}$ 的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2023八下·永善期末) 如图，在平行四边形ABCD中，AB⊥AC，若AB=8，AC=12，则BD的长是（）

A . 22 B . 16 C . 18C D . 20

答案解析收藏纠错 + 选题
9. (2023八下·永善期末) 如图，矩形ABCD中，E、F、M为AB、BC、CD边上的点，且AB=6，BC=7，AE=3，DM=2，EF⊥FM，则EM的长为（）

A . 5 B . 5 $\text{[math]}$ C . 6 D . 6 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023八下·永善期末) 如图，一次函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象相，交于点P(m，4)，则关于x、y的二元一次方程组 $\text{[math]}$ 的解是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023六上·宁阳期中) 计算： $\text{[math]}$ ， …归纳各计算结果中的个位数字规律，猜测 $\text{[math]}$ 的个位数字是（）

A . 1 B . 3 C . 7 D . 5

答案解析收藏纠错 + 选题
12. (2023八下·永善期末) 如图，分别以B△ABC的斜边AB，直角边AC为边向外作等边△ABD和等边△ACE，F为AB的中点，DE、AB相交于点G，若 $\text{[math]}$ ，下列结论：
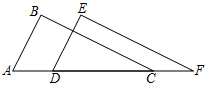
①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④△DBF≌△EFA。
其中正确结论的个数有（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题(本大题共4小题，每小题2分，共8分)

13. (2023八下·永善期末) 函数 $\text{[math]}$ 的自变量x的取值范围是.

答案解析收藏纠错 + 选题
14. (2024九下·巴彦模拟) 分解因式： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
15. (2023八下·永善期末) 已知整数a使得不等式组 $\text{[math]}$ 的解集为 $\text{[math]}$ ，且使得一次函数 $\text{[math]}$ 的图象不经过第四象限，则整数a的值为。

答案解析收藏纠错 + 选题
16. (2023八下·永善期末) 如下图，在△ABC中，AB=AC，BC=6，△ABC面积为12，AD⊥BC于点D，直线EF垂直平分AB交AB于点E，交BC于点F，P为直线EF上一动点，则△PBD的周长的最小值为。

答案解析收藏纠错 + 选题

三、解答题(本大题共8小题，共56分)

17. (2023八下·永善期末) 计算： $\text{[math]}$ 。

答案解析收藏纠错 + 选题
18. (2023八下·永善期末) 如图，点A，D，C，F在同一条直线上，AD＝CF，AB＝DE，AB∥DE.求证：BC＝EF.

答案解析收藏纠错 + 选题
19. (2023八下·永善期末) 在△ABC中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求△ABC的面积。

答案解析收藏纠错 + 选题
20. (2023八下·永善期末) 如图，在平面直角坐标系中，A(3，4)，B(1，2)，C(5，1)。
1. （1）在图中作出△ABC关于y轴的对称图形 $\text{[math]}$ ；
2. （2）写出点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的坐标(直接写答案)
  $\text{[math]}$ ：， $\text{[math]}$ ：； $\text{[math]}$ ：。
3. （3）求△ABC的面积。
答案解析收藏纠错 + 选题

21. (2023八下·永善期末) 2023年6月26日是“国际禁毒日”，某中学组织七、八年级全体学生开展了“禁毒知识”网上竞赛活动.为了解竞赛情况，从两个年级各随机抽取了10名同学的成绩(满分为100分)，收集数据为：

七年级90，95，95，80，90，80，85，90，85，100；

八年级85，85，95，80，95，90，90，90，100，90。

整理数据：

	80	85	90	95	100
七年级	2	2	3	2	1
八年级	1	2	4	a	1

分析数据：

	平均数	中位数	众数	方差
七年级	89	b	90	39
八年级	c	90	d	300

根据以上信息回答下列问题：

（1）请直接写出表格中a，b，c，d的值；
（2）通过数据分析，你认为哪个年级的成绩比较好？请说明理由；
（3）该校七、八年级共有600人，本次竞赛成绩不低于90分的为“优秀”。估计这两个年级共有多少名学生达到“优秀”？

答案解析收藏纠错 + 选题

22. (2023八下·永善期末) 如图，已知四边形ABCD是平行四边形，并且 $\text{[math]}$ 。
1. （1）求证：四边形ABCD为矩形；
2. （2）点E是AB边的中点，F为AD边上一点. $\text{[math]}$ ，若CE=4，CF=5，求DF的长。
答案解析收藏纠错 + 选题
23. (2023八下·永善期末) 某商场准备购进A、B两种书包，每个A种书包比B种书包的进价少20元，用700元购进A种书包的个数是用450元购进B种书包个数的2倍，A种书包每个标价是90元，B种书包每个标价是130元。请解答下列问题：
1. （1） A、B两种书包每个进价各是多少元？
2. （2）若该商场购进B种书包的个数比A种书包的2倍还多5个，且A种书包不少于18个，购进A、B两种书包的总费用不超过5450元，则该商场有哪几种进货方案？
3. （3）该商场按(2)中获利最大的方案购进书包，在销售前，拿出5个书包赠送给某希望小学，剩余的书包全部售出，其中两种书包共有4个样品，每种样品都打五折，商场仍获利1370元。请直接写出赠送的书包和样品中，B种书包各有几个？
答案解析收藏纠错 + 选题
24. (2023八下·永善期末) 如图，在平面直角坐标系中，点A、B分别在x轴、y轴上，线段OA、OB的长(OA<OB)是方程组 $\text{[math]}$ 的解，点C是直线 $\text{[math]}$ 与直线AB的交点，点D在线段OC上， $\text{[math]}$ 。
1. （1）求点C的坐标；
2. （2）求直线AD的解析式；
3. （3） P是直线AD上的点，在平面内是否存在点Q，使以O、A、P、Q为顶点的四边形是菱形？若在(在，请写出点Q的坐标：若不存在，请说明理由。
答案解析收藏纠错 + 选题