

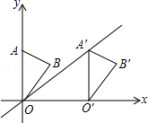
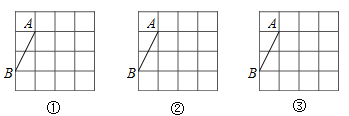
.(写出一个即可)

30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
整理数据:
课外阅读平均时间(x分钟) | 0 | 40 | 80 | 120 |
人数 | 3 | 5 | a | 4 |
分析数据:
平均数 | 中位数 | 众数 |
80 | m | n |
请根据以上提供的信息,解答下列问题:

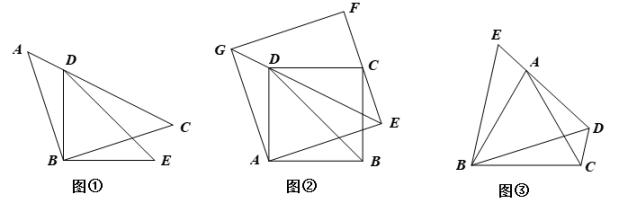
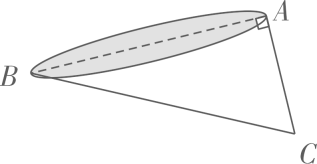
【问题提出】如图①,△ABC和△DBE都是等腰直角三角形,∠ABC=∠DBE=90°,
点D在AC上.求证:AD2+CD2=DE2. 通过连接CE,得AD=CE,∠ACE=90°. 从而
得出△DCE为直角三角形,使问题得证.
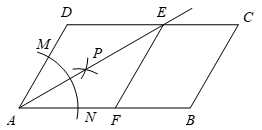
∠ADC= °;若AD=6,AE=2,则△ACD的面积为 .
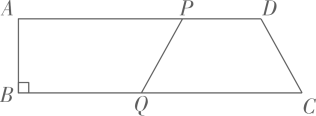
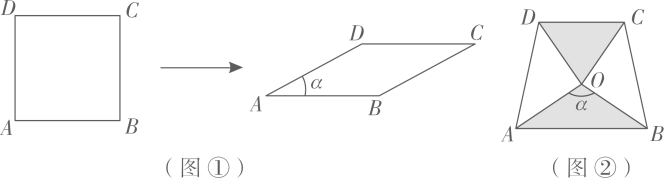
α | 30° | 45° | 60° | 90° | 120° | 135° | 150° |
S | | 1 | | |
例如:当α=30°时,S=S(30°)= , 当α=135°时,S=S(135°)=
.
由上表可以得到S(60°)=S(°),S(30°)=S(°),…,由此
可以归纳出S(α)=S().
求证:S△DOC=S△AOB.