北京市通州区2023年2023年中考一模数学考试试卷

更新时间：2023-10-12 浏览次数：69 类型：中考模拟

一、选择题（本大题共8小题，共16.0分。在每小题列出的选项中，选出符合题目的一项）

1. (2023·通州模拟) 下列图形： $\text{[math]}$ 线段； $\text{[math]}$ 角； $\text{[math]}$ 等边三角形； $\text{[math]}$ 平行四边形 $\text{[math]}$ 其中既是轴对称图形又是中心对称图形的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·通州模拟) $\text{[math]}$ 年 $\text{[math]}$ 月国家统计局网站数据显示， $\text{[math]}$ 年全国居民人均消费支出 $\text{[math]}$ 元，将 $\text{[math]}$ 用科学记数法表示（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023八上·朝阳期中) 如图，一副三角板拼成如图所示图形，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023·通州模拟) 正七边形的外角和为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·通州模拟) 如图是某个几何体的表面展开图，则这个几何体是（）

A . 长方体 B . 三棱柱 C . 三棱锥 D . 四棱锥

答案解析收藏纠错 + 选题
6. (2023·通州模拟) 点 $\text{[math]}$ ， $\text{[math]}$ 在数轴上的位置如图所示，点 $\text{[math]}$ ， $\text{[math]}$ 表示的有理数为 $\text{[math]}$ ， $\text{[math]}$ 如果 $\text{[math]}$ ， $\text{[math]}$ ，那么下列描述数轴原点的位置说法正确的是（）

A . 原点 $\text{[math]}$ 在点 $\text{[math]}$ 左侧 B . 原点 $\text{[math]}$ 在点 $\text{[math]}$ 的右侧 C . 原点 $\text{[math]}$ 在点 $\text{[math]}$ 、 $\text{[math]}$ 之间，且 $\text{[math]}$ D . 原点 $\text{[math]}$ 在点 $\text{[math]}$ 、 $\text{[math]}$ 之间，且 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·夏县月考) 如图 $\text{[math]}$ ，一个均匀的转盘被平均分成 $\text{[math]}$ 等份，分别标有 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 小凯转动转盘做频率估计概率的实验，当转盘停止转动后，指针指向的数字即为实验转出的数字，图 $\text{[math]}$ ，是小凯记录下的实验结果情况，那么小凯记录的实验是（）

A . 转动转盘后，出现偶数 B . 转动转盘后，出现能被 $\text{[math]}$ 整除的数
C . 转动转盘后，出现比 $\text{[math]}$ 大的数 D . 转动转盘后，出现能被 $\text{[math]}$ 整除的数

答案解析收藏纠错 + 选题
8. (2023·通州模拟) 如图，在平面直角坐标系 $\text{[math]}$ 中，四边形 $\text{[math]}$ 是一个矩形，小球 $\text{[math]}$ 从点 $\text{[math]}$ 出发沿直线向点 $\text{[math]}$ 运动，到达点 $\text{[math]}$ 时被第一次反弹，每当小球 $\text{[math]}$ 沿直线运动碰到矩形的边时反弹，反弹时反射角等于入射角，当小球 $\text{[math]}$ 第 $\text{[math]}$ 次碰到矩形的边时，小球 $\text{[math]}$ 所在位置的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共8小题，共16.0分）

9. (2024九下·北京市月考) 若代数式 $\text{[math]}$ 有意义，那么 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题
10. (2024九下·北京市模拟) 分解因式 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2023·通州模拟) 已知 $\text{[math]}$ 为整数，且 $\text{[math]}$ ，则 $\text{[math]}$ 等于．

答案解析收藏纠错 + 选题
12. (2023·通州模拟) 方程 $\text{[math]}$ 的解是．

答案解析收藏纠错 + 选题
13. (2023·通州模拟) 由电源、开关、滑动变阻器及若干导线组成的串联电路中，已知电源电压为定值，闭合开关后，改变滑动变阻器的阻值 $\text{[math]}$ 始终保持 $\text{[math]}$ ，发现通过滑动变阻器的电流 $\text{[math]}$ 与滑动变阻器的电阻 $\text{[math]}$ 成反比例函数关系，它的图象如图所示，若使得通过滑动变阻器的电流不超过 $\text{[math]}$ ，则滑动变阻器阻值的范围是．

答案解析收藏纠错 + 选题

14. (2023·通州模拟) 为探究浸种处理对花生种子萌发率的影响，九年级的生物小组同学取 $\text{[math]}$ 粒花生种子完成实验 $\text{[math]}$ 同学们将 $\text{[math]}$ 粒花生种子平均分成五组，获得如下花生种子萌发量数据，如表格．

组别处理	花生种子萌发量 $\text{[math]}$ 单位：粒 $\text{[math]}$
组别处理	第 $\text{[math]}$ 组	第 $\text{[math]}$ 组	第 $\text{[math]}$ 组	第 $\text{[math]}$ 组	第 $\text{[math]}$ 组
浸种 $\text{[math]}$ 小时、 $\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

在温度 $\text{[math]}$ 的条件下，将 $\text{[math]}$ 粒种子浸种 $\text{[math]}$ 小时，萌发量大致为粒 $\text{[math]}$

答案解析收藏纠错 + 选题

15. (2023·通州模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，将一个直角尺 $\text{[math]}$ 的直角顶点 $\text{[math]}$ 与 $\text{[math]}$ 边上的中点 $\text{[math]}$ 重合，并绕点 $\text{[math]}$ 旋转，分别交 $\text{[math]}$ 、 $\text{[math]}$ 于点 $\text{[math]}$ 、 $\text{[math]}$ ，如果四边形 $\text{[math]}$ 恰巧是正方形，则 $\text{[math]}$ 的长度为．

答案解析收藏纠错 + 选题
16. (2023·通州模拟) 某学校带领 $\text{[math]}$ 名学生到农场参加植树劳动，学校同时租用 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种型号客车去农场，其中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种型号客车载客量分别为 $\text{[math]}$ 人、 $\text{[math]}$ 人、 $\text{[math]}$ 人，租金分别为 $\text{[math]}$ 元、 $\text{[math]}$ 元、 $\text{[math]}$ 元 $\text{[math]}$ 为了节省资金，学校要求每辆车必须满载，并将学生一次性送到农场植树，请你写出一种满足要求的租车方案，满足要求的几种租车方案中，最低租车费用是元 $\text{[math]}$

答案解析收藏纠错 + 选题

三、解答题（本大题共12小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）

17. (2023·通州模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2023·通州模拟) 解不等式组 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2023·通州模拟) 先化简，再求值：已知 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题

20. (2023·通州模拟) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点，请你用无刻度的直尺
在图中画 $\text{[math]}$ 的边 $\text{[math]}$ 上的高线 $\text{[math]}$ 小蕊的画法如下 $\text{[math]}$ 请你按照小器的画法完成画图，并填写证明的依据．

画法：
$\text{[math]}$ 连接 $\text{[math]}$ ，
$\text{[math]}$ 连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，
$\text{[math]}$ 连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，
$\text{[math]}$ 作射线 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，
$\text{[math]}$ 即为所求 $\text{[math]}$ 的边 $\text{[math]}$ 上的高线
证明：
$\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点，
$\text{[math]}$ ．
$\text{[math]}$ ，
$\text{[math]}$ 四边形 $\text{[math]}$ 是平行四边形．     ▲   ．
$\text{[math]}$ 点 $\text{[math]}$ 是 $\text{[math]}$ 中点．     ▲   ．
$\text{[math]}$ 、 $\text{[math]}$ 是 $\text{[math]}$ 的中线．
$\text{[math]}$ 是 $\text{[math]}$ 的中线．
$\text{[math]}$ ，
$\text{[math]}$ 是 $\text{[math]}$ 边上的高线．     ▲   ．

答案解析收藏纠错 + 选题

21. (2023·通州模拟) 已知在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ ， $\text{[math]}$ 中点，连接 $\text{[math]}$ ， $\text{[math]}$ ，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）如果 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
22. (2023·通州模拟) 如图，平面直角坐标系 $\text{[math]}$ 中，一次函数 $\text{[math]}$ 的图象 $\text{[math]}$ 分别与 $\text{[math]}$ ， $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，正比例函数 $\text{[math]}$ 的图象 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的值及 $\text{[math]}$ 的表达式；
2. （2）一次函数 $\text{[math]}$ 的图象为 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三条直线不能围成三角形，直接写出所有满足条件的 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
23. (2023·通州模拟) 北极海冰是地球系统的重要组成部分，其变化可作为全球气候变化的重要指示器 $\text{[math]}$ 为了应对全球气候问题，科学家运用卫星遥感技术对北极海冰覆盖面积的变化情况进行监测，根据对多年的数据进行整理、描述和分析，形成了如下信息：
$\text{[math]}$ 、 $\text{[math]}$ 年间北极海冰年最低覆盖面积变化的频数分布直方图如下所示： $\text{[math]}$ 数据分成 $\text{[math]}$ 组： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

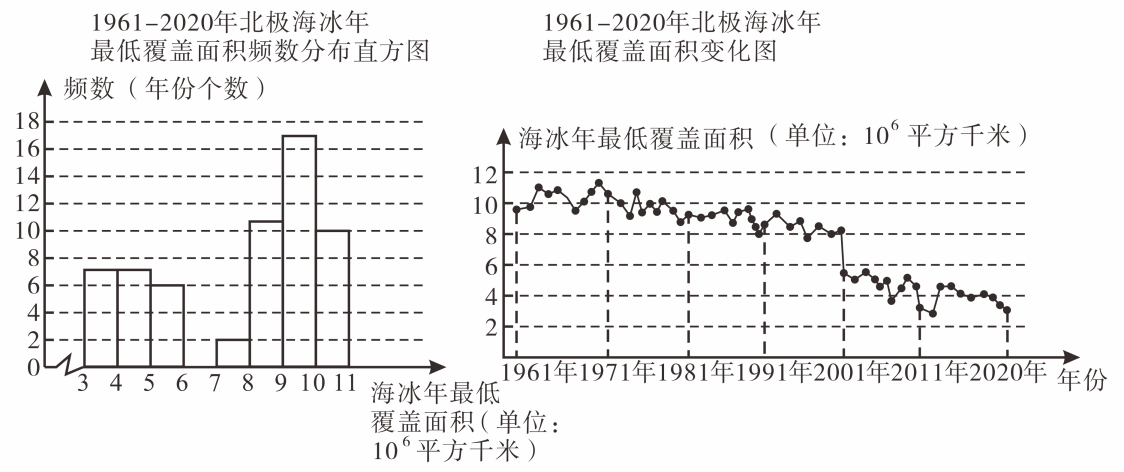
$\text{[math]}$ 、 $\text{[math]}$ 年间北极海冰年最低覆盖面积的数据在 $\text{[math]}$ 这一组的是： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
1. （1）写出 $\text{[math]}$ 年间北极海冰年最低覆盖面积的中位数是 ▲ $\text{[math]}$ 平方千米 $\text{[math]}$ ；
2. （2）北极海冰最低覆盖面积出现了大面积的缩减是 ▲ 年 $\text{[math]}$
3. （3）请参考反映 $\text{[math]}$ 年间北极海冰年最低覆盖面积变化的折线图，解决以下问题：
  $\text{[math]}$ 记北极地区 $\text{[math]}$ 年北极海冰年最低覆盖面积的方差为 $\text{[math]}$ ， $\text{[math]}$ 年北极海冰年最低覆盖面积的方差为 $\text{[math]}$ ，请直接判断 $\text{[math]}$ ▲ $\text{[math]}$ 的大小关系 $\text{[math]}$ 填写“ $\text{[math]}$ ”“ $\text{[math]}$ ”或“ $\text{[math]}$ ” $\text{[math]}$ ；
  $\text{[math]}$ 根据 $\text{[math]}$ 年以后北极海冰年最低覆盖面积的相关数据，推断全球气候发生了怎样的变化？在你的生活中应采取哪些措施应对这一变化？
答案解析收藏纠错 + 选题
24. (2023·通州模拟) 如图， $\text{[math]}$ 是圆内接三角形，过圆心 $\text{[math]}$ 作 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ 是 $\text{[math]}$ 的切线；
2. （2）如果 $\text{[math]}$ ，求 $\text{[math]}$ 半径的长度．
答案解析收藏纠错 + 选题

25. (2023·通州模拟) 如图， $\text{[math]}$ 是学校灌溉草坪用到的喷水设备，喷水口 $\text{[math]}$ 离地面垂直高度为 $\text{[math]}$ 米，喷出的水流都可以抽象为平面直角坐标系中的一条抛物线．

（1）灌溉设备喷出水流的最远射程可以到达草坪的最外侧边沿点 $\text{[math]}$ ，此时，喷水口 $\text{[math]}$ 喷出的水流垂直高度与水平距离的几组数据如下表．

水平距离 $\text{[math]}$ 米	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
竖直高度 $\text{[math]}$ 米	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

结合数据，求此抛物线的表达式，并求出水流最大射程 $\text{[math]}$ 的长度．

（2）为了全面灌溉，喷水口 $\text{[math]}$ 可以喷出不同射程的水流，喷水口 $\text{[math]}$ 喷出的另外一条水流形成的抛物线满足表达式 $\text{[math]}$ ，此水流最大射程 $\text{[math]}$ 米，求此水流距离地面的最大高度．

答案解析收藏纠错 + 选题

26. (2023·通州模拟) 在平面直角坐标系 $\text{[math]}$ 中，已知点 $\text{[math]}$ ， $\text{[math]}$ 在二次函数 $\text{[math]}$ 的图象上．
1. （1）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值；
2. （2）当 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
27. (2023·通州模拟) 直线 $\text{[math]}$ 是线段 $\text{[math]}$ 的垂直平分线，垂足为点 $\text{[math]}$ ，点 $\text{[math]}$ 是直线 $\text{[math]}$ 上一点，连接 $\text{[math]}$ 以 $\text{[math]}$ 为斜边作等腰直角 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）如图 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
2. （2）如图 $\text{[math]}$ 所示，点 $\text{[math]}$ 是射线 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，连接 $\text{[math]}$ ，延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使得 $\text{[math]}$ ，连接 $\text{[math]}$ ，根据题意补全图 $\text{[math]}$ ，写出线段 $\text{[math]}$ ， $\text{[math]}$ 之间的关系，并证明．
答案解析收藏纠错 + 选题
28. (2023·通州模拟) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，给出如下定义：作直线 $\text{[math]}$ 分别交 $\text{[math]}$ ， $\text{[math]}$ 边于点 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 关于直线 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，则称 $\text{[math]}$ 为等腰直角 $\text{[math]}$ 关于直线 $\text{[math]}$ 的“直角对称点” $\text{[math]}$ 点 $\text{[math]}$ 可与点 $\text{[math]}$ 重合，点 $\text{[math]}$ 可与点 $\text{[math]}$ 重合 $\text{[math]}$
1. （1）在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ ： $\text{[math]}$ ， $\text{[math]}$ 为等腰直角 $\text{[math]}$ 关于直线 $\text{[math]}$ 的“直角对称点”．
  $\text{[math]}$ 当 $\text{[math]}$ 时，写出点 $\text{[math]}$ 的坐标；
  $\text{[math]}$ 连接 $\text{[math]}$ ，求 $\text{[math]}$ 长度的取值范围；
2. （2） $\text{[math]}$ 的半径为 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点，以点 $\text{[math]}$ 为直角顶点作等腰直角 $\text{[math]}$ ，其中 $\text{[math]}$ ，直线 $\text{[math]}$ 与 $\text{[math]}$ 、 $\text{[math]}$ 分别交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，同时 $\text{[math]}$ 为等腰直角 $\text{[math]}$ 关于直线 $\text{[math]}$ 的“直角对称点”，连接 $\text{[math]}$ ，当点 $\text{[math]}$ 在 $\text{[math]}$ 上运动时，直接写出 $\text{[math]}$ 长度的最大值与最小值．
答案解析收藏纠错 + 选题