安徽省合肥市蜀山区合肥市琥珀中学2023-2024学年八年级...

更新时间：2024-01-15 浏览次数：31 类型：期中考试

一、选择题（本大题共10小题，每小题3分，共30分）

1. (2023八上·蜀山期中) 平面直角坐标系中，点 $\text{[math]}$ 所在象限是（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
2. (2023八上·蜀山期中) 函数 $\text{[math]}$ 中自变量 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 且 $\text{[math]}$ D . $\text{[math]}$ 且 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
3. (2023八上·蜀山期中) 如图，在△ABC中，BC边上的高为（）

A . AD B . BE C . BF D . CG

答案解析收藏纠错 + 选题
4. (2023八上·蜀山期中) 对于一次函数 $\text{[math]}$ ，下列说法不正确的是（）

A . 图象与 $\text{[math]}$ 的图象平行 B . 图像不经过第三象限 C . 图象与坐标轴围成的面积是2 D . 当 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023八上·蜀山期中) 在 $\text{[math]}$ 中，若 $\text{[math]}$ ，则 $\text{[math]}$ 是（）

A . 锐角三角形 B . 直角三角形 C . 钝角三角形 D . 不确定

答案解析收藏纠错 + 选题
6. (2023八上·蜀山期中) 一次函数 $\text{[math]}$ 的图像，可由函数 $\text{[math]}$ 的图像（）

A . 向左平移2个单位长度而得到 B . 向右平移2个单位长度而得到 C . 向上平移2个单位长度而得到 D . 向下平移2个单位长度而得到 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023八上·蜀山期中) 一次函数 $\text{[math]}$ 的图象过点 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 和 $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无法确定

答案解析收藏纠错 + 选题
8. (2023八上·蜀山期中) 如图，一次函数 $\text{[math]}$ 与 $\text{[math]}$ 的图像交于点P，下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③当 $\text{[math]}$ 时， $\text{[math]}$ ；④ $\text{[math]}$ ；⑤ $\text{[math]}$ ．所有正确结论的序号为（）．

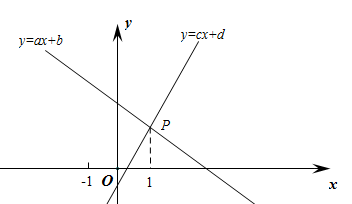
A . ①②③ B . ①②④ C . ②③⑤ D . ②④⑤

答案解析收藏纠错 + 选题
9. (2023八上·蜀山期中) 如图，已知在 $\text{[math]}$ 中， $\text{[math]}$ ，点D沿 $\text{[math]}$ 自B向C运动，作 $\text{[math]}$ 于E， $\text{[math]}$ 于F，则 $\text{[math]}$ 的值y与 $\text{[math]}$ 的长x之间的函数图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. (2023八上·蜀山期中) 如图，在平面直角坐标系中，线段 $\text{[math]}$ 的端点坐标为 $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 与线段 $\text{[math]}$ 有交点，则 $\text{[math]}$ 的值不可能是（）

A . －5 B . －2 C . 3 D . 5

答案解析收藏纠错 + 选题

二、填空题（本大题共5小题，每小题4分，共20分）

11. (2023八上·蜀山期中) 若一个等腰三角形的两边长分别为4和10，则这个三角形的周长．

答案解析收藏纠错 + 选题
12. (2023八上·蜀山期中) 已知直线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于 $\text{[math]}$ 轴上一点，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2023八上·蜀山期中) 当三角形中一个内角α是另一个内角β的一半时，我们称此三角形为“半角三角形”，其中α称为“半角”．如果一个“半角三角形”的“半角”为25°，那么这个“半角三角形”的最大内角的度数为．

答案解析收藏纠错 + 选题
14. (2023八上·蜀山期中) 若函数 $\text{[math]}$ ，则当函数值 $\text{[math]}$ 时，自变量 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
15. (2023八上·蜀山期中) $\text{[math]}$ 取任意值，直线 $\text{[math]}$ 恒过一定点，则该点的坐标是，平面直角坐标系中有三点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若该直线 $\text{[math]}$ 将 $\text{[math]}$ 分成左右面积之比为 $\text{[math]}$ 的两部分，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题

三、解答题（本大题共7小题，16－18每题6分，19－22每题8分，共50分）

16. (2023八上·蜀山期中) 已知函数 $\text{[math]}$
1. （1）若函数图象经过原点，求 $\text{[math]}$ 的值；
2. （2）若函数的图象平行于直线 $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
17. (2023八上·蜀山期中) 如图，在平面直角坐标系中，三角形 $\text{[math]}$ 各顶点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．将三角形 $\text{[math]}$ 向右平移5个单位长度，再向上平移3个单位长度得到三角形 $\text{[math]}$ ．
1. （1）写出点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的对应点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的坐标；
2. （2）画出平移后的三角形 $\text{[math]}$ ；
3. （3）在平面直角坐标系中，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ．将点 $\text{[math]}$ 先向右平移5个单位长度，再向上移3个单位长度后得到点 $\text{[math]}$ ，则 $\text{[math]}$ 点坐标是；
答案解析收藏纠错 + 选题
18. (2023八上·蜀山期中) 如图所示，已知 $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ 的高和中线， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的长．
2. （2）求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
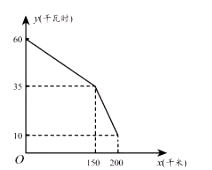
19. (2024八下·荔湾期中) 如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量 $\text{[math]}$ （千瓦时）关于已行驶路程 $\text{[math]}$ （千米）的函数图象.
1. （1）根据图象，直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程，当 $\text{[math]}$ 时，求1千瓦时的电量汽车能行驶的路程；
2. （2）当 $\text{[math]}$ 时求 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式，并计算当汽车已行驶180千米时，蓄电池的剩余电量.
答案解析收藏纠错 + 选题
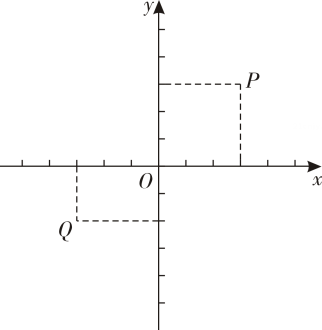
20. (2023八上·蜀山期中) 在平面直角坐标系 $\text{[math]}$ 中，对于 $\text{[math]}$ ， $\text{[math]}$ 两点给出如下定义：若点 $\text{[math]}$ 到 $\text{[math]}$ 、 $\text{[math]}$ 轴的距离中的最大值等于点 $\text{[math]}$ 到 $\text{[math]}$ 、 $\text{[math]}$ 轴的距离中的最大值，则称 $\text{[math]}$ ， $\text{[math]}$ 两点为“等距点”．如图中的 $\text{[math]}$ ， $\text{[math]}$ 两点即为“等距点”．
备用图
1. （1）已知点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，在点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 中，为点 $\text{[math]}$ 的“等距点”的是．
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ 两点为“等距点”，且两点纵坐标异号，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
21. (2023八上·蜀山期中) 某超市鸡蛋供应紧张，需每天从外地调运鸡蛋600千克．超市决定从甲、乙两大型养殖场调运鸡蛋，已知甲养殖场每天最多可调出400千克，乙养殖场每天最多可调出450千克，从甲、乙两养殖场调运鸡蛋到该超市的路程和运费如表：

到超市的路程（千米）
运费（元/千克·千米）
甲养殖场
90
0.05
乙养殖场
40
0.03
设从甲养殖场调运鸡蛋 $\text{[math]}$ 千克，总运费为 $\text{[math]}$ 元．
1. （1）从甲养殖场调运鸡蛋的运费，用代数式表示为，从乙养殖场需要调运鸡蛋的数量，用代数式表示为；
2. （2）试写出 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式；
3. （3）请求出自变量取值范围，说明怎样安排调运方案才能使每天的总运费最少？
答案解析收藏纠错 + 选题
22. (2023八上·蜀山期中) 如图，直线 $\text{[math]}$ 与坐标轴交于点 $\text{[math]}$ 、 $\text{[math]}$ 两点，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于点 $\text{[math]}$ ，交 $\text{[math]}$ 轴于点 $\text{[math]}$ ，且 $\text{[math]}$ 的面积为 $\text{[math]}$ ．
1. （1）则 $\text{[math]}$ 点的坐标为； $\text{[math]}$ ；
2. （2）求直线 $\text{[math]}$ 的解析式；
3. （3）若点 $\text{[math]}$ 是线段 $\text{[math]}$ 上一动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题