江西省抚州市东乡区2023-2024学年七年级上学期数学期中...

更新时间：2024-03-12 浏览次数：24 类型：期中考试

一、选择题（本大题共6小题，每小题3分，共18分）

1. (2024七上·岚山期末) $\text{[math]}$ 的相反数为（）

A . 2023 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023七上·东乡区期中) 在下列各数：﹣（+2），﹣3² ， $\text{[math]}$ 中，负数有（　　）个．

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
3. (2023七上·东乡区期中) 某几何体的表面展开图如图所示，这个几何体是（）

A . 圆柱 B . 长方体 C . 四棱锥 D . 五棱锥

答案解析收藏纠错 + 选题
4. (2023七上·东乡区期中) 中国古代十进位制的算筹记数法在世界数学史上是一个伟大的创造．据史料推测，算筹最晚出现在春秋晚期战国初年.1至9这9个数字的纵式和横式的表示数码如下图所示，算筹记数的方法为：个位用纵式，十位用横式，百位再用纵式，千位再用横式…，以此类推，就可以用算筹表示出任意大的自然数了．
根据上述材料， $\text{[math]}$ 的运算结果可用算筹表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023七上·东乡区期中) 如图所示，数轴上点A、B对应的有理数分别为a、b ，下列说法正确的是（　　）

A . ab＞0 B . a+b＞0 C . |a|﹣|b|＜0 D . a﹣b＜0

答案解析收藏纠错 + 选题
6. (2023七上·东乡区期中) 如图是一个运算程序的示意图，若第一次输入x的值为81，则第2023次输出的结果为（）

A . 27 B . 9 C . 3 D . 1

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分）

7. (2023七上·东乡区期中) 单项式 $\text{[math]}$ 的系数是.

答案解析收藏纠错 + 选题
8. (2023七上·东乡区期中) 正方体的截面中，边数最多的是边形．

答案解析收藏纠错 + 选题
9. (2023七上·东乡区期中) 据国土资源部数据显示，我国是全球“可燃冰”资源储量最多的国家之一，海、陆总储量约为39000000000吨油当量，将39000000000用科学记数法表示为。

答案解析收藏纠错 + 选题
10. (2023七上·东乡区期中) 若单项式－5x²y^a与－2x^by⁵的和仍为单项式，则这两个单项式的和为

答案解析收藏纠错 + 选题
11. (2023七上·东乡区期中) 如图，图形都是由同样大小的“〇”按一定的规律组成其中第1个图形中一共有5个“〇”，第2个图形中一共有12个“〇”，第3个图形中一共有21个“〇”，……，则第10个图形中“〇”的个数是．

答案解析收藏纠错 + 选题
12. (2023七上·东乡区期中) 若a是绝对值最小的数，b是最大的负整数，c的立方等于本身，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

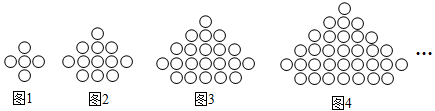
三、解答题（本大题共5小题，每小题6分，共30分）

13. (2023七上·东乡区期中) 计算：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
14. (2023七上·东乡区期中) 先化简，再求值． $\text{[math]}$ ．其中 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2023七上·东乡区期中) 在数轴上画出表示下列各数的点，并用“<”将这些数连接起来．
$\text{[math]}$

答案解析收藏纠错 + 选题
16. (2023七上·东乡区期中) 如图是由9个小正方体搭成的立体图形，在网格中画出从正面、从左面和从上面观察该几何体看到的形状图.

答案解析收藏纠错 + 选题
17. (2023七上·东乡区期中) 设a、b都表示有理数，规定一种新运算“※”：当 $\text{[math]}$ 时， $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ ．例如： $\text{[math]}$ ， $\text{[math]}$ ．
1. （1） $\text{[math]}$ ；
2. （2）求 $\text{[math]}$ 的值；
答案解析收藏纠错 + 选题

四、解答题（本大题共3小题，每小题8分，共24分）

18. (2024七上·南山期中) 已知 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点在数轴上对应的位置如图所示.
1. （1）若 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ .
2. （2）化简： $\text{[math]}$
答案解析收藏纠错 + 选题
19. (2023七上·东乡区期中) 出租车司机小李某天上午运营全是在某条南北走向的路上进行的，如果规定向北为正，向南为负，这天上午他的行车里程（单位：千米）如下：﹣6.5，+5，﹣7，+10，+6.5，﹣9．
1. （1）将最后一位乘客送到目的地时，小李在出发点（南/北）千米；
2. （2）若汽车耗油量为0.2升/千米，小李接送这六位乘客，出租车共耗油多少升？
3. （3）小李师傅接到第三位乘客后，刚好遇上高峰期，遇红灯及堵车等候时间约为32分钟，问第三位乘客需支付车费多少元？
  
  起步价（3千米以内）
  超过3千米部分每千米费用（不足1千米以1千米计）
  等候费（不足1分钟以1分钟计）
  （单价：元）
  11
  2.5
  每4分钟2.5元
答案解析收藏纠错 + 选题
20. (2024七上·苏州月考) 已知代数式 $\text{[math]}$ ， $\text{[math]}$
1. （1）求 $\text{[math]}$ 的值；
2. （2）若 $\text{[math]}$ 值与 $\text{[math]}$ 的取值无关，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题

五、解答题（本大题共2小题，每小题9分，共18分）

21. (2023七上·东乡区期中) 阅读材料：“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．例如：已知 $\text{[math]}$ ，则代数式 $\text{[math]}$ ．请根据以上材料解答下列问题：
1. （1）若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为；
2. （2）当 $\text{[math]}$ 时，代数式 $\text{[math]}$ 的值是5，求当 $\text{[math]}$ 时，代数式 $\text{[math]}$ 的值；
3. （3）当 $\text{[math]}$ 时，代数式 $\text{[math]}$ 的值为 $\text{[math]}$ ，求当 $\text{[math]}$ 时，代数式 $\text{[math]}$ 的值（用含 $\text{[math]}$ 的式子表示）．
答案解析收藏纠错 + 选题
22. (2023七上·东乡区期中) 双11网络促销活动即将到来，甲、乙两家网店分别出售A型、B型两种取暖器，零售价及运费如下表所示：
型号
网店
A型
B型
运费
A型
B型
甲
100元/台
200元/台
10元/台
10元/台
乙
120元/台
190元/台
免运费
12元/台
某公司计划在网上采购A型、B型两种取暖器共10台，其中A型取暖器购买x台．
1. （1）若两种取暖器全部在甲网店购买，需付总费用为元（用含x的最简式子表示）；若两种取暖器全部在乙网店购买，需付总费用为元（用含x的最简式子表示）；
2. （2）当 $\text{[math]}$ 时，请通过计算解决下列问题：
  ①在（1）中的条件下，该公司在哪家网店购买取暖器更划算？
  ②若两种取暖器可以同时在两家网店自由选择购买，还有比①中更优惠的方案吗？如果有，请写出这个方案，并求出此时购买取暖器的总费用；如果没有，请说明理由．
答案解析收藏纠错 + 选题

六、解答题（本大题共12分）

23. (2023七上·东乡区期中) 已知数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ，请回答问题：
1. （1）请直接写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的值： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）数轴上 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三个数所对应的点分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ 两点的距离可表示为 $\text{[math]}$ ，数轴上有一点 $\text{[math]}$ ，它表示的数为 $\text{[math]}$ 若 $\text{[math]}$ ，则点 $\text{[math]}$ 表示的数 $\text{[math]}$ 是；
3. （3）点 $\text{[math]}$ 和点 $\text{[math]}$ 分别以每秒 $\text{[math]}$ 个单位长度和 $\text{[math]}$ 个单位长度的速度同时向右运动，设运动时间为 $\text{[math]}$ ．
  $\text{[math]}$ 当 $\text{[math]}$ 时，求 $\text{[math]}$ 的长；
  $\text{[math]}$ 当 $\text{[math]}$ ， $\text{[math]}$ 两点的距离为 $\text{[math]}$ 时，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

江西省抚州市东乡区2023-2024学年七年级上学期数学期中...

副标题：

*注意事项：

江西省抚州市东乡区2023-2024学年七年级上学期数学期中...

试题分析

总体分析

题量分析

难度分析

知识点分析

	起步价（3千米以内）	超过3千米部分每千米费用（不足1千米以1千米计）	等候费（不足1分钟以1分钟计）
（单价：元）	11	2.5	每4分钟2.5元

型号网店	A型	B型	运费
型号网店	A型	B型	A型	B型
甲	100元/台	200元/台	10元/台	10元/台
乙	120元/台	190元/台	免运费	12元/台