题库组卷系统-专注K12在线组卷服务

在线咨询

当前：初中数学

当前位置：初中数学 /中考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

浙江省温州市苍南县苍南中学2023-2024学年九年级上学期...

更新时间：2024-03-29 浏览次数：131 类型：中考模拟

一、选择题(本大题共7小题，每小题6分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的)

1. (2023九上·苍南模拟) 已知实数a满足 $\text{[math]}$ + $\text{[math]}$ =a，那么a- $\text{[math]}$ 的值是（）

A . 2023 B . -2023 C . 2024 D . -2024

答案解析收藏纠错 + 选题
2. (2023九上·苍南模拟) 设k为非负实数，且方程 $\text{[math]}$ -2kx+4=0的两实数根为a，b，则 $\text{[math]}$ + $\text{[math]}$ 的最小值为（）

A . -7 B . -6 C . 2 D . 4

答案解析收藏纠错 + 选题
3. (2023九上·苍南模拟) 如图，在三角形ABC中，AB=11，AC=15，点M是BC的中点，AD是∠BAC的角平分线，MF∥AD，则FC=（）

A . 14 B . 13 C . 12 D . 11

答案解析收藏纠错 + 选题
4. (2023九上·苍南模拟) 设直线nx+(n+1)y= $\text{[math]}$ (n为自然数)与两坐标轴围成的三角形面积为 $\text{[math]}$ (n=1，2，3，..，2023).则 $\text{[math]}$ + $\text{[math]}$ +…+ $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·苍南模拟) 若实数x，y满足|x|+4|y|=1，则m=y-4x的最大值是（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
6. (2023九上·苍南模拟) 已知n(n≥8)个正实数 $\text{[math]}$ ， $\text{[math]}$ ， ···， $\text{[math]}$ 满足 $\text{[math]}$ = $\text{[math]}$ ，其中q是不为1的正数.则 $\text{[math]}$ + $\text{[math]}$ ，与 $\text{[math]}$ + $\text{[math]}$ 的大小关系为（）

A . 大于 B . 等于 C . 小于 D . 不能确定

答案解析收藏纠错 + 选题
7. (2023九上·苍南模拟) 已知正整数a，b，c满足2a=b+270，a+7c=6b，则a的最小值为（）

A . 141 B . 153 C . 160 D . 174

答案解析收藏纠错 + 选题

二、填空题(本题有7个小题,每小题6分，共42分)

8. (2023九上·苍南模拟) 已知x为实数，且满足 $\text{[math]}$ -12=0，那么 $\text{[math]}$ -x+1的值为.

答案解析收藏纠错 + 选题
9. (2024九下·绵阳模拟) 某电脑公司经销甲种型号电脑，受经济危机影响，电脑价格不断下降，今年三月份的电脑售价比去年同期每台降价1000元。如果卖出相同数量的电脑，去年销售额为10万元，今年销售额只有8万元.则今年三月份甲种电脑每台售价为元.

答案解析收藏纠错 + 选题
10. (2023九上·苍南模拟) 函数y= $\text{[math]}$ - $\text{[math]}$ - $\text{[math]}$ 的最大值为.

答案解析收藏纠错 + 选题
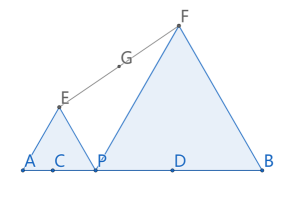
11. (2023九上·苍南模拟) 如图，已知AB=8，点C、D在线段AB上且AC=1，DB=3，P是线段CD上的动点，分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB，连结EF，设EF的中点为G，当点P从点C运动到点D时，则点G移动路径的长是.

答案解析收藏纠错 + 选题
12. (2023九上·苍南模拟) 二次函数y= $\text{[math]}$ -2ax+a在0≤x≤2上有最小值-6，则a的值为.

答案解析收藏纠错 + 选题
13. (2023九上·苍南模拟) 若实数a.b满足 $\text{[math]}$ + $\text{[math]}$ =1， $\text{[math]}$ + $\text{[math]}$ =1，则a+b=.

答案解析收藏纠错 + 选题
14. (2023九上·苍南模拟) 如图，矩形ABCD中，AB=1，BC=2，AE为∠BAD的平分线，F为AE上一动点，点M为DF的中点，连接BM，则BM的最小值是.

答案解析收藏纠错 + 选题

三、解答题(本大题共3题,共36分.解答应写出文字说明、证明过程或演算步骤)

15. (2023九上·苍南模拟) 如图，已知在平面直角坐标系中，点P的坐标为(5，5)，射线PA与x轴正半轴交于点A、射线PB与y轴正半轴交于点B.若∠APB=45°，则△AOB的周长是否会发生变化?若不变，求出△AOB的周长；若变化，请说明理由.

答案解析收藏纠错 + 选题
16. (2023九上·苍南模拟)
1. （1）已知方程① $\text{[math]}$ + $\text{[math]}$ = $\text{[math]}$ ， ② $\text{[math]}$ + $\text{[math]}$ + $\text{[math]}$ =3请判断这两个方程是否有解?并说明理由；
2. （2）已知 $\text{[math]}$ + $\text{[math]}$ =2023，求 $\text{[math]}$ 的值。
答案解析收藏纠错 + 选题
17. (2023九上·苍南模拟) 我们把自变量为x的函数记作f(x)，f(x。)表示自变量x=x。时，函数f(x)的值.已知函数f(x)= $\text{[math]}$ -4x+6.
1. （1）当-1≤x≤1时，不等式f(x)≥2x+2m+1恒成立，求实数m的取值范围；
2. （2）设函数g(x)=x+b，若对任意1≤ $\text{[math]}$ ≤4，存在5≤ $\text{[math]}$ ≤8，使得g( $\text{[math]}$ )=f( $\text{[math]}$ )，求实数b的取值范围。
答案解析收藏纠错 + 选题

试卷信息