一、单项选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项符合要求.
-
-
-
A .  B .
B .  C . 2
D . 4
C . 2
D . 4
-
A . 8
B . 9
C . 10
D . 11
-
A . -2
B . -1
C . 1
D . 
-
6.
(2023高一上·吉林期末)
科学家以里氏震级来度量地震的强度,若设
Ⅰ为地震时所散发出来的相对能量程度,则里氏震级
y可定义为

, 2021年3月13日下午江西鹰潭余江区发生里氏3.1级地震,2020年1月1日四川自贡发生里氏4.9级地震,则自贡地震所散发出来的能量是余江地震所散发出来的能量的( )倍.
A . 2
B . 10
C . 100
D . 1000
-
-
-
-
二、多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
-
A . 函数 的定义域是
的定义域是 B . 函数
B . 函数 在其定义域上单调递减
C . 函数
在其定义域上单调递减
C . 函数 的值域是
的值域是 D . 函数
D . 函数 的图象过定点
的图象过定点
-
A . 若命题“ ,
,  ”为假命题,则实数
”为假命题,则实数 的取值范围是
的取值范围是 B . 若
B . 若 , 则“
, 则“ ”的充要条件是“
”的充要条件是“ ”
C . “
”
C . “ ”是“
”是“ ”的充分不必要条件
D . 当
”的充分不必要条件
D . 当 时,
时, 的最小值为
的最小值为
-
-
A . 函数 在
在 上单调递减
B . 函数
上单调递减
B . 函数 的最小正周期是
的最小正周期是 C . 函数
C . 函数 的图象向左平移
的图象向左平移 个单位后关于直线
个单位后关于直线 对称
D . 若圆半径为
对称
D . 若圆半径为 , 则函数
, 则函数 的解析式为
的解析式为
三、填空题:本大题共6个小题,每小题5分,共30分.
四、解答题:共50分.解答应写出文字说明,证明过程或演算步骤.
-
-
-
(2)
正实数
a ,
b满足

, 求

的最小值.
-
22.
(2023高一上·吉林期末)
某公司设计了某款新产品,为生产该产品需要引进新型设备.已知购买该新型设备需要3万元,之后每生产
x万件产品,还需另外投入原料费及其他费用

万元,产量不同其费用也不同,且

已知每件产品的售价为8元且生产的该产品可以全部卖出.
-
(1)
写出年利润

(万元)关于年产量
x(万件)的函数解析式;
-
(2)
该产品年产量为多少万件时,公司所获年利润最大?其最大利润为多少万元?
-
-
(1)
求函数

的单调递增区间,对称中心;、
-
(2)
将函数

的图象上所有点的横坐标伸长为原来的4倍,纵坐标不变,再将所得图象向左平移

个单位,得到函数

的图象,并求函数

在

的值域.
-
-
-
(1)
求

的值;
-
(2)
若

使不等式

成立,求实数
m的取值范围;
-
(3)
设

, 若

有三个不同的实数解,求实数
k的取值范围
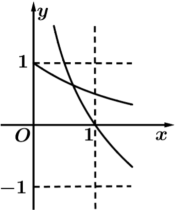 B .
B . 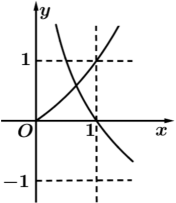 C .
C . 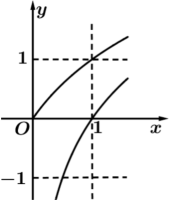 D .
D .