贵州省黔东南州从江县东朗中学2023-2024学年七年级上学...

更新时间：2024-04-09 浏览次数：53 类型：月考试卷

一、选择题:以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,每小题3分,共36分.

1. (2023七上·从江月考) - $\text{[math]}$ 的倒数是（）

A . 2 024 B . -2 024 C . $\text{[math]}$ D . - $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023七上·从江月考) 下列几何体中，是棱锥的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023七上·从江月考) 森林是地球之肺，每年能为人类提供大约28.3亿吨的有机物，28.3亿用科学记数法表示为（）

A . 28.3×10⁷ B . 2.83×10⁸ C . 0.283×10¹⁰ D . 2.83×10⁹

答案解析收藏纠错 + 选题
4. (2023七上·从江月考) 单项式- $\text{[math]}$ xy²的系数、次数分别为（）

A . $\text{[math]}$ ， 2 B . - $\text{[math]}$ ， 2 C . - $\text{[math]}$ ， 3 D . -2，3

答案解析收藏纠错 + 选题
5. (2023七上·从江月考) 已知x=3是关于x的方程2x-a=1的解，则a的值是（）

A . -5 B . 5 C . 7 D . 2

答案解析收藏纠错 + 选题
6. (2023七上·从江月考) 下列运算正确的是（）

A . 4m-m=3 B . 2a³-3a³=-a³ C . a²b-ab²=0 D . yx-2xy=xy

答案解析收藏纠错 + 选题
7. (2023七上·从江月考) 根据等式的性质，下列等式变形中，不一定成立的是（）

A . 若x=y，则x+2=y+2 B . 若x=y，则1-x=1-y C . 若ax=ay，则x=y D . 若 $\text{[math]}$ = $\text{[math]}$ ，则x=y

答案解析收藏纠错 + 选题
8. (2023七上·从江月考) 如图所示的是正方体的一种平面展开图，各面都标有数字，则数字为-2的面与其对面上的数字之积是（）

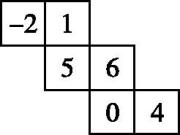
A . -12 B . 0 C . -8 D . -10

答案解析收藏纠错 + 选题
9. (2023七上·从江月考) 中国古代人民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有个问题：今有三人共车，二车空；二人共车，九人步，问人与车各几何?这道题的意思是：今有若干人乘车，每3人乘一车，最终剩余2辆车；若每2人共乘一车，最终剩余9个人无车可乘，问有多少人，多少辆车?如果我们设有x辆车，那么可列方程（）

A . 3(x-2)=2x+9 B . 3(x+2)=2x-9 C . $\text{[math]}$ +2= $\text{[math]}$ D . $\text{[math]}$ -2= $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023七上·从江月考) 如图所示，长为12 cm的线段AB的中点为M，C将线段MB分为MC和CB，且MC∶MB=1∶3，则线段AC的长为（）

A . 2 cm B . 8 cm C . 6 cm D . 4 cm

答案解析收藏纠错 + 选题
11. (2023七上·从江月考) 将一副直角三角尺按如图所示的不同方式摆放，则图中∠α与∠β互余的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
12. (2023七上·从江月考) 如图所示，把周长为3个单位长度的圆放到数轴(单位长度为1)上，A，B，C三点将圆三等分，将点A与数轴上表示1的点重合，然后将圆沿着数轴正方向滚动，依次为点B与数轴上表示2的点重合，点C与数轴上表示3的点重合，点A与数轴上表示4的点重合……若当圆停止运动时点B正好落到数轴上，则点B对应的数轴上的数可能为（）

A . 2 020 B . 2 021 C . 2 022 D . 2 023

答案解析收藏纠错 + 选题

二、填空题:每小题4分,共16分.

13. (2023七上·从江月考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2023七上·从江月考) 若x，y为实数，且|x+2|+(y-2)²=0，则( $\text{[math]}$ )^{2 021}的值为.

答案解析收藏纠错 + 选题
15. (2023七上·从江月考) 一个角的余角比它的补角的一半还少20°，则这个角的度数为.

答案解析收藏纠错 + 选题
16. (2023七上·从江月考) 我国春秋时期的《大戴礼》，记载了世界上最早的“幻方”[如图(1)(2)所示]，该“幻方”中，每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等.现有如图(2)所示的“幻方”，则(x-y)^m-n的值是.

答案解析收藏纠错 + 选题

三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.

17. (2023七上·从江月考) 计算：
1. （1） 100÷2²- $\text{[math]}$ ×[3-(-3)²]；
2. （2） -1^{2 023}+24÷(-2)³-3²×( $\text{[math]}$ )².
答案解析收藏纠错 + 选题
18. (2023七上·从江月考) 解下列方程：
1. （1） -2(x-1)=3x+2；
2. （2） $\text{[math]}$ - $\text{[math]}$ =-1.
答案解析收藏纠错 + 选题
19. (2023七上·从江月考) 先化简，再求值：(8mn-3m²)-5mn-2(3mn-2m²)，其中m=-1，n=2.

答案解析收藏纠错 + 选题
20. (2023七上·从江月考) 如图所示，已知线段AB.
1. （1）请用尺规按下列要求作图：
  ①延长线段AB到C，使BC=AB；
  ②延长线段BA到D，使AD=AC.(不写画法，但要保留画图痕迹)
2. （2）请直接回答线段BD与线段AC长度之间的大小关系.
3. （3）如果AB=2 cm，请求出线段BD和CD的长度.
答案解析收藏纠错 + 选题
21. (2023七上·从江月考) 如图所示，已知长方形ABCD的宽AB=6，以B为圆心，AB长为半径画弧与边BC交于点E，连接DE.若CE=x.(计算结果保留π)
1. （1）用含x的代数式表示图中阴影部分的面积；
2. （2）当x=4时，求图中阴影部分的面积.
答案解析收藏纠错 + 选题
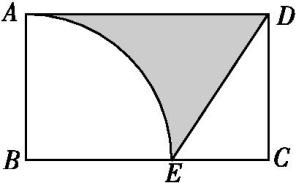
22. (2023七上·从江月考) 某校七年级社会实践小组去商场调查商品销售情况，了解到该商场以每件80元的价格购进了某品牌衬衫500件，并以每件120元的价格销售了400件，商场准备采取促销措施，将剩下的衬衫降价销售．请你帮商场计算一下，每件衬衫降价多少元时，销售完这批衬衫正好达到盈利45%的预期目标？

答案解析收藏纠错 + 选题
23. (2023七上·从江月考) 出租车司机小张某天在路(近似地看成一条直线)上行驶，如果规定向东为“正”，向西为“负”，他这天上午的行程可以表示为+5，-3，+3，-1，+2，-2，+4，-5，+6，-8(单位：km).
1. （1）小张将最后一名乘客送达目的地后需要返回出发地换班，请问小张该如何行驶才能回到出发地?
2. （2）汽车耗油量为0.08 L/ km，发车前油箱有31.2 L汽油，若小张将最后一名乘客送达目的地，再返回出发地，小张今天上午是否需要加油?若需要加油，至少需要加多少才能返回出发地?若不需要加油，请说明理由.
答案解析收藏纠错 + 选题
24. (2023七上·从江月考) 将连续的奇数1，3，5，7，9，…排成如图所示的数阵，用十字框按如图所示的方式任意框五个数.(十字框只能平移)
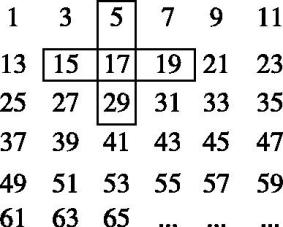
1. （1）若框住的五个数中，正中间的一个数为17，则这五个数的和为.
2. （2）十字框内五个数的和的最小值是.
3. （3）设正中间的数为a，用式子表示十字框内五个数的和.
4. （4）十字框能否框住这样的五个数，它们的和等于2035?若能，求出正中间的数a；若不能，请说明理由.
答案解析收藏纠错 + 选题
25. (2023七上·从江月考) 综合与实践
【问题情境】利用旋转开展数学活动，探究体会角在旋转过程中的变化.
【操作发现】如图(1)所示，∠AOB=∠COD=90°且两个角重合.
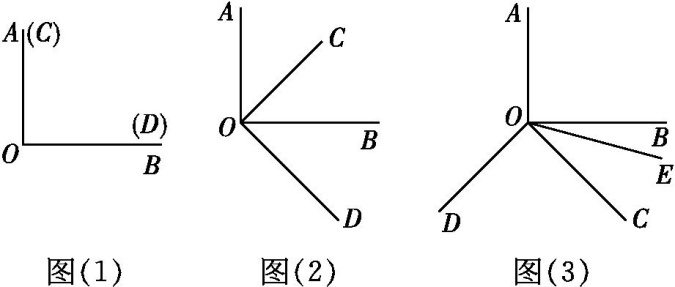
1. （1）将∠COD绕着顶点O顺时针旋转45°如图(2)所示，此时OB平分；∠BOC的余角有个(本身除外)，分别是.
2. （2）【实践探究】
  将∠COD绕着顶点O顺时针继续旋转如图(3)位置，若∠BOC=45°，射线OE在∠BOC内部，且∠BOC=3∠BOE.请探究：
  ①∠BOC的补角有 ▲ 个，分别是 ▲ ；
  ②求∠DOE的度数.
答案解析收藏纠错 + 选题