一、选择题:以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,每小题3分,共36分.
-
A . 调查某山中的红腹锦鸡数量
B . 了解贵阳市中学生的睡眠情况
C . 调查全国中学生视力和用眼卫生情况
D . 检查我国发射的“神舟十四号”载人飞船各零部件的情况
-
2.
(2024七上·贵阳月考)
2021年5月15日7时18分，执行我国首次火星探测任务的“天问一号”探测器在火星着落，在火星上首次留下中国印迹.火星是太阳系八大行星之一，火星的半径约为3 395 000 m，3 395 000这个数用科学记数法可表示为（ ）
A . 33.95×105
B . 3.395×105
C . 3.395×106
D . 0.339 5×107
-
A . 水下91 m
B . 水下31 m
C . 水下60 m
D . 水下29 m
-
-
A . 3a+2b=5ab
B . 4m2n-2mn2=2mn
C . -12x+7x=-5x
D . 5y2-3y2=2
-
6.
(2024七上·贵阳月考)
黄果树风景区到关岭县城的坝陵河大桥建成后，从黄果树风景区到关岭县城经大桥通过的路程缩短20 km，用所学数学知识解释这一现象恰当的是（ ）
A . 两点确定一条直线
B . 两点之间线段最短
C . 垂线段最短
D . 连接两点间线段的长度是两点间的距离
-
7.
(2024七上·贵阳月考)
2022年2月20日下午，随着男子冰球决赛结束，冬奥会最终奖牌榜出炉，中国队用他们的拼搏和汗水，创造了历史最佳战绩，共获得9枚金牌、4枚银牌、2枚铜牌，现在要制作一种统计图表示中国队获得的各项奖牌数目，最适合的统计图是（ ）
A . 折线统计图
B . 条形统计图
C . 扇形统计图
D . 以上三种都适合
-
A . 方程3x-2=2x+1，移项，得3x-2x=1+2
B . 方程
-
=1，去分母，得2-3(x-1)=1
C . 方程3-x=2-5(x-1)，去括号，得3-x=2-5x-1
D . 方程23x=32，系数化为1，得x=1
-
A . a-b<0
B . |a|<|b|
C . a+b>0
D . ab>0
-
10.
(2024七上·贵阳月考)
如图所示，若点A，O，B在一条直线上，OM平分∠AOC，∠BON∶∠CON=1∶4，当∠AOM=20°时，∠CON等于（ ）
A . 112°
B . 132°
C . 28°
D . 140°
-
-
12.
(2024七上·贵阳月考)
一个白色圆生成一个黑色圆，一个黑色圆生成一个白色圆和一个黑色圆，按如图所示的方式排列，以此类推，第十行圆有（ ）
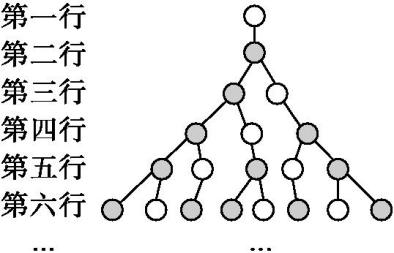
A . 55个
B . 30个
C . 89个
D . 34个
二、填空题:每小题4分,共16分.
-
-
-
-
16.
(2024七上·贵阳月考)
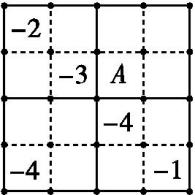
如图所示的是一个宫格图，图中实线划分的区域是一个宫，共有4个宫，每一宫又被虚线分为四个小格.根据图中已经给的提示数字，在其他的空格上填入数字-1，-2，-3，-4.使-1，-2，-3，-4每个数字在每一行、每一列和每一宫中都只出现一次.则图中点A位置所填的数字为
.
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
-
-
-
-
（2）
-1=
.
-
19.
(2024七上·贵阳月考)
由6个棱长相等的正方体组成的几何体如图所示.在指定的方格内画出该几何体从三个方向看到的形状图.
-
20.
(2024七上·贵阳月考)
一出租车一天下午以某广场为出发点在南北方向营运，向北为正，向南为负，行车里程(单位：km)依先后次序记录如下：+9，-3，-5，+4，+6，+3，-6，-4.
-
（1）
将最后一名乘客送到目的地，出租车离该广场出发点多远?
-
（2）
若每千米的价格为2.4元，司机该天下午的营业额是多少?
-
21.
(2024七上·贵阳月考)
某服装店销售一款衬衣，按进价提高80%标价销售.国庆期间搞促销活动，按标价的6折出售.顾客购买一件该衬衣，结算时可使用店铺免费派发的10元优惠券，此时店铺仍可获利14元.请求出该款衬衣每件的进价.
-
22.
(2024七上·贵阳月考)
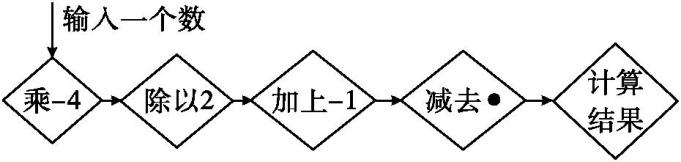
如图所示，某数学活动小组编制了一道有理数混合运算题，即输入一个有理数，按照自左向右的顺序运算，可得计算结果，其中“
”表示一个有理数.
-
-
（2）
若计算结果为8，且输入的数是4，则表示的数是多少?
-
（3）
若输入的数为a，表示的数为b，当计算结果为0时，求出a与b之间的数量关系.
-
23.
(2024七上·贵阳月考)
阅读材料：我们知道，4x-2x+x=(4-2+1)x=3x，类似地，我们把(a+b)看成一个整体，则4(a+b)-2(a+b)+(a+b)=(4-2+1)(a+b)=3(a+b).“整体思想”是中学学习中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛.
尝试应用：
-
（1）
把(a-b)2看成一个整体，合并3(a-b)2-6(a-b)2+2(a-b)2的结果是；
-
（2）
已知x2-2y=4，求3x2-6y-21的值；
-
（3）
拓展探索：
已知a-2b=3，2b-c=-5，c-d=10，求(a-c)+(2b-d)-(2b-c)的值.
-
24.
(2024七上·贵阳月考)
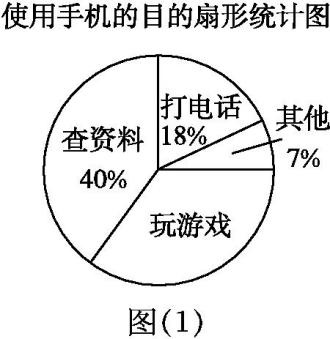
教育部办公厅印发了《关于加强中小学生手机管理的工作通知》，要求中小学生原则上不得将个人手机带入校园，确有需求的，须经家长同意、书面提出申请，进校后应将手机由学校统一保管，禁止带入课堂.为了解学生手机使用情况，某学校开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查，并绘制成如图(1)，图(2)所示的统计图，已知“查资料”的人数是48人.
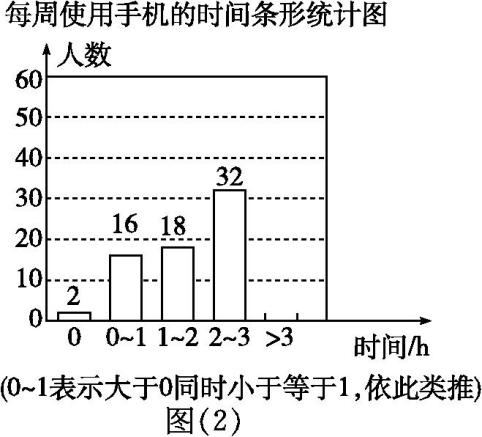
解答下列问题：
-
（1）
在扇形统计图中，表示“玩游戏”的扇形圆心角度数为， 补全条形统计图；
-
（2）
该校共有学生2 100人，估计每周使用手机时间在2 h以上(不含2 h)的人数；
-
-
-
（1）
[知识初探]
如图(1)所示，若∠AOB=58°，求∠BOC的度数；
-
（2）
[类比再探]
折叠长方形纸片，OC，OD均是折痕，折叠后，点A落在点A′，点B落在点B′，连接OA′.如图(2)所示，当点B′在OA′上时，判断∠AOC与∠BOD的关系，并说明理由；
-
（3）
[类比探究]
如图(3)所示，在图(2)的基础上，当点B′在∠COA′的内部时，连接OB′.若∠AOC=44°，∠BOD=61°，求∠A′OB′的度数.
”表示一个有理数.
