一、单选题(本大题共12小题,每小题3分,每小题只有一个正确答案,共36分)
-
A . ﹣3
B . ﹣  C . 3
D .
C . 3
D . 
-
A . x+y=3
B .  C . 2x﹣x=0
D . 2x﹣x
C . 2x﹣x=0
D . 2x﹣x
-
A . 3.2×104升
B . 3.2×105升
C . 3.2×106升
D . 3.2×107升
-
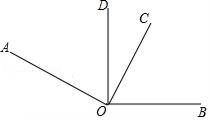
A . 25°
B . 65°
C . 47°
D . 75°
-
A . ﹣m2n4
B . mn4
C . ﹣m7n
D . 5m3n2
-
6.
(2024七上·鹿寨期末)
关于补角有下列四个叙述:①锐角的补角是钝角;②只有锐角才有补角;③互为补角的两个角不可能相等;④同角或等角的补角一定相等.其中正确的个数有( )
A . 1个
B . 2个
C . 3个
D . 4个
-
A . 45°
B . 55°
C . 65°
D . 75°
-
A . b<﹣a<﹣b<a
B . b<﹣b<﹣a<a
C . b<﹣a<a<﹣b
D . ﹣a<﹣b<b<a
-
A . - B .
B .  C . ﹣3
D . 3
C . ﹣3
D . 3
-
-
11.
(2024七上·鹿寨期末)
船在静水中的速度为27千米/时,水流速度为3千米/时,从甲码头顺流而行到乙码头再返回甲码头,共用了4.5小时(中途不停留),设甲、乙两码头的行程为x千米,则下面所列方程正确的是( )
A . (27+3)x=4.5
B .  C .
C .  D . (27+3)x+(27﹣3)(4.5﹣x)=1
D . (27+3)x+(27﹣3)(4.5﹣x)=1
-
12.
(2024七上·鹿寨期末)
如图,在数轴上,点A,B分别表示﹣15,9,点P,Q分别从点A,B同时开始沿数轴正方向运动,点P的速度是每秒3个单位,点Q的速度是每秒1个单位,运动时间为t秒,在运动过程中,当点P,点Q和原点O这三点中的一点恰好是另外两点为端点的线段的中点时,则满足条件整数t的值( )
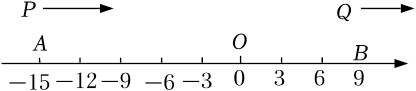
A . 22
B . 33
C . 44
D . 55
二、填空题(本大题共6小题,每小题2分,共12分,请将答案直接填写在题中的横线。)
-
-
-
-
16.
(2024七上·鹿寨期末)
“双十一”期间,某商家把一款书包先按原来售价提高50%,然后再打八折出售,这样商家每卖出一个书包比原来还要多赚8元.若设此款书包原来售价是x元,由题意可列方程为
.(不要求化简)
-
17.
(2024七上·鹿寨期末)
如图1是某景区电动升降门,将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,当CD平行于地面AE时,则∠ABC+∠BCD=
.

-
18.
(2024七上·鹿寨期末)
如图,已知△ABC中,∠CAB=20°,∠ABC=30°,将△ABC绕A点逆时针旋转50°得到△AB
'C
' , 以下结论:①BC=B
'C
' , ②AC平分∠BAB
' , ③∠BAB
'=∠CAC
' , ④AC∥C
'B
' , 其中正确结论的序号是
.

三、解答题(本大题共7题,解答时应写出必要的解题过程,共72分)
-
-
20.
(2024七上·鹿寨期末)
先化简,再求值:8a
2﹣10ab+2b
2﹣(2a
2﹣10ab+8b
2),其中a=

, b=﹣

.
-
-
(1)
同时过

,

,两点能作几条直线?作图并写出理由;
-
(2)
在直线

上画出符合下列条件的点

和

,并说明理由.
①使线段  长度最小;
长度最小;
②使  最小.
最小.
-
22.
(2024七上·鹿寨期末)
如图,用三种大小不同的5个正方形和1个长方形(阴影部分)拼成长方形ABCD,其中EF=3,最小的正方形的边长为x.

-
-
-
-
23.
(2024七上·鹿寨期末)
某机械厂计划平均每天生产300个零件,但是由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超过计划量记为正):
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
+6 | ﹣2 | ﹣8 | +10 | ﹣7 | +5 | +4 |
-
(1)
根据记录的数据,求该厂星期二生产零件多少个?
-
(2)
根据记录的数据,求产量最多的一天比产量最少的一天多生产零件多少个?
-
(3)
根据记录的数据,求该厂本周实际共生产零件多少个?
-
24.
(2024七上·鹿寨期末)
为了增强市民的节约用水意识,自来水公司实行阶梯收费,具体情况如表:
每月用水量 | 收费 |
不超过10吨的部分 | 水费1.6元/吨 |
10吨以上至20吨的部分 | 水费2元/吨 |
20吨以上的部分 | 水费2.4元/吨 |
-
(1)
若小刚家6月份用水15吨,则小刚家6月份应缴水费 26元.(直接写出结果)
-
(2)
若小刚家7月份的平均水费为1.75元/吨,则小刚家7月份的用水量为多少吨?
-
(3)
若小刚家8月、9月共用水40吨,9月底共缴水费79.6元,其中含2元滞金(水费为每月底缴纳.因8月份的水费未按时缴,所以收取了滞纳金),已知9月份用水比8月份少,求小明算8、9月各用多少吨水?
-
-
26.
(2024七上·鹿寨期末)
如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)

-
(1)
如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE=;
-
(2)
如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;
-
(3)
如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.

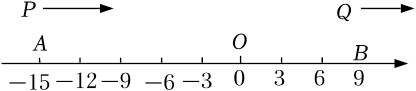


长度最小;
最小.