一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
-
-
-
-
A . 了解一叠钞票中有没有假钞
B . 调查神州17号载人飞船零部件的情况
C . 调查一批圆珠笔芯的使用寿命
D . 调查班上同学早餐是否有喝牛奶的习惯
-
-
-
A . 过两点有且只有一条直线
B . 多项式 的次数是5
C . 用一个平面去截三棱柱,截面可能是六边形
D . 连接两点的线段叫做这两点间的距离
的次数是5
C . 用一个平面去截三棱柱,截面可能是六边形
D . 连接两点的线段叫做这两点间的距离
-
8.
(2024七上·邛崃期末)
某电影院所有大厅可容纳的人数相同,所有小厅可容纳的人数也相同。2个大厅和1个小厅共可同时容纳1960人观影;1个大厅和2个小厅共可同时容纳1460人观影.如果设一个大厅可同时容纳
y人观影,由题意列出的方程正确的是( )
二、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
-
-
10.
(2024七上·邛崃期末)
冰箱启动时内部的温度为6℃,在冰箱的降温范围内,如果每一小时冰箱内部的温度降低4℃,那么2小时后冰箱内部的温度为
℃.
-
-
12.
(2024七上·邛崃期末)
神州17号载人飞船已于2023年10月26日上午11时14分成功发射.上午11时14分时钟上时针与分针的夹角是
.
-
13.
(2024七上·邛崃期末)
某商店出售两件衣服,每件售240元,其中一件亏本20%,而另一件盈利20%,则这两件衣服在这次销售中的利润是
元.
三、解答题(本大题共5个小题,共48分,解答过程写在答题卡上)
-
-
(1)
计算:

-
(2)
解方程:

, 并判断所求出的未知数的值是否是原方程的解,请写出判断过程.
-
-
(1)
求

的度数;
-
-
16.
(2024七上·邛崃期末)
2023年,成都市积极响应教育部关于开展课后服务的号召,各校给学生提供了丰富多彩的课后活动.其中某校开展了以下体育项目:篮球,乒乓球,足球和羽毛球.该校每个学生都只选择参加其中一项活动.某调查组为了解该校选择各项体育活动的学生人数,随机抽取了部分学生进行调查,并将获得的数据进行了整理,绘制出了以下两幅不完整的统计图:

根据图中提供的信息,回答下列问题:
-
(1)
该调查组本次调查的学生人数是人,并补全条形统计图;
-
(2)
选择足球项目的人数在扇形统计图中对应的圆心角度数为;
-
(3)
若该学校有学生2400人,请你估计该学校学生选择篮球项目的人数约有多少人?
-
-
(1)
若

, 求线段
DF的长;
-
(2)
若线段CE的长恰好等于线段DF的一半,求线段CE的长;
-
(3)
如图2,取线段DE的中点M , 线段CF的中点N , 求线段MN的长.
-
18.
(2024七上·邛崃期末)
乘坐滴滴快车是一种便捷的出行方式,其计价规则如下表:
计费项目 | 里程费 | 时长费 | 远途费 |
单价 | 1.6元/公里 | 0.4元/分钟 | 0.6元/公里 |
注:车费由里程费、时长费、远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程8公里以内(含8公里)不收远途费,超过8公里的,超出部分每公里另加收0.6元. |
-
(1)
若张老师乘坐滴滴快车,行车里程为5公里,行车时间为8分钟,则需付车费多少元;
-
(2)
若刘老师乘坐滴滴快车,行车里程为m公里,行车时间为n分钟,则刘老师应付车费多少元;
-
(3)
小聪与小敏各自乘坐滴滴快车,乘车里程分别为7.5公里与9公里,并且两人下车时所付车费相同,请问小聪的行车时间与小敏的行车时间有何关系?
四、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
-
-
20.
(2024七上·邛崃期末)
一个几何体由若干大小相同的小立方块搭成,下图分别是从正面、上面看到的形状图,则搭成这个几何体的小立方块最多有
个.

-
21.
(2024七上·邛崃期末)
我们知道无限循环小数是有理数,有理数包括整数和分数,任何一个无限循环小数都可以写成分数或整数的形式,应该怎样写呢?我们以无限循环小数

为例进行说明:设

, 由

;可知

, 而

, 所以

, 解得

, 于是得

. 按此方法,将

写成分数(或整数)的形式是
,将

写成分数(或整数)的形式是
.
-
22.
(2024七上·邛崃期末)
古代数学问题趣题,如图,一个瓶子的容积为1200 cm
3 , 瓶内装着一些溶液.当瓶子正放时,瓶内溶液恰好为瓶子圆柱体部分,液体高度为24 cm,当瓶子倒放时,空余部分圆柱体的高度为6 cm.则瓶内溶液的体积为
cm
3 .

-
23.
(2024七上·邛崃期末)
如图,点
G为直线
EF上一点,

, 将

绕点
G逆时针旋转,当射线
GA与射线
GE重合时停止旋转;在旋转过程中,射线
GC始终平分

;当
GB ,
GC ,
GE三条射线中有一条是另外两条射线所成夹角的平分线时,

的度数为
.

五、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)
-
24.
(2024七上·邛崃期末)
【阅读】有一种整式处理器,能将二次多项式处理成一次多项式,处理方法是:将二次多项式的二次项的未知数次数二次变为一次,再将其二次项的系数乘以2保留,将二次多项式的一次项去掉未知数只保留其系数,将二次多项式的常数项去掉.例如:二次多项式

, 二次多项式
A经过处理器处理得到一次二项式

.
【应用】若关于x的二次多项式A经过处理器处理得到一次二项式B , 根据以上方法,解决下列问题:
-
(1)
若

, 则
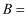
;
-
(2)
若

, 求关于
y的方程

的解;
-
(3)
【延伸】
已知 , A是关于y的二次多项式,若B是A经过处理器得到的关于y的一次二项式,求关于y的方程
, A是关于y的二次多项式,若B是A经过处理器得到的关于y的一次二项式,求关于y的方程 的解.
的解.
-
-
(1)
如图1,已知点
M ,
N是线段
CD上两点,且

, 点
E和点
F分别是线段
CN和线段
DM的中点.若线段

, 分别求线段

,

,

的长;
-
(2)
已知
OM ,
ON是从

的顶点发出的两条射线,

且

, 射线
OE和射线
OF分别平分

,

.
①如图2,若OM , ON均为 内的两条射线,且
内的两条射线,且 , 求
, 求 的度数;
的度数;
②如图3,若OM为 外的一条射线,且
外的一条射线,且 , 则
, 则 ▲ .
▲ .
-
-
(1)
请直接写出
a ,
b的值:

,

;
-
(2)
数轴上
a ,
b ,
x三个数所对应的点分别为
A、
B、
X , 且点
X是数轴上的任意点,点
A与点
X之间的距离用
AX表示,点
B与点
X之间的距离用
BX表示,请计算当
x分别为

, 0,2025时,代数式

的值,并指出当

的值最小时,点
X在数轴上的位置;
-
(3)
如果在数轴连续的整数点上依次有n个机器人,且相邻两个机器人之间的距离都是1个单位,同时数轴上有一个快递包裹分发点智能机器人,它能根据机器人的数量自动决策出快递包裹分发点的位置,使得每个机器人去取快递包裹的距离之和最小,请直接用含n的代数式表示这个最小值.
 B .
B .  C .
C .  D .
D . 
![]()




, A是关于y的二次多项式,若B是A经过处理器得到的关于y的一次二项式,求关于y的方程
的解.

内的两条射线,且
, 求
的度数;
外的一条射线,且
, 则
▲ .