浙江省杭州市萧山区高桥初中教育集团2023-2024学年第二...

更新时间：2024-04-17 浏览次数：15 类型：月考试卷

一、选择题：本大题有10个小题, 每小题3分, 共30分. 在每小题给出的四个选项中, 只有一个选项是符合要求的.

1. (2023七上·余姚期中) 2023年9月23日晚，杭州亚运会开幕式现场，超过1.05亿名线上火炬手汇聚而成的“数字火炬手”与现场真实的火炬手一起，共同点燃亚运之火，创造了新的吉尼斯世界纪录．其中数据1.05亿用科学记数法可表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八上·玉环期末) 下列运算结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024九下·萧山月考) 某市身高不超过 $\text{[math]}$ 的儿童可以免费乘坐公共汽车，若可以免费乘坐公共汽车儿童的身高为 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九下·萧山月考) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九下·萧山月考) 如图，是一个正方体的展开图，若相对面上的两个数互为相反数，则代数式 $\text{[math]}$ 的值是（）

A . 6 B . $\text{[math]}$ C . 18 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九下·萧山月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ ，点P为 $\text{[math]}$ 上一动点，若 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
7. (2024九下·萧山月考) 如图，用大小形状完全相同的长方形纸片在直角坐标系中摆成如图所示的图案，已知 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
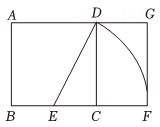
8. (2024九下·萧山月考) 黄金分割由于其美学性质，受到摄影爱好者和艺术家的喜爱，摄影中有一种拍摄手法叫黄金构图法．其原理是：如图，将正方形 $\text{[math]}$ 的底边 $\text{[math]}$ 取中点E ，以E为圆心，线段 $\text{[math]}$ 为半径作圆，其与底边 $\text{[math]}$ 的延长线交于点F ，这样就把正方形 $\text{[math]}$ 延伸为矩形 $\text{[math]}$ ，称其为黄金矩形．若 $\text{[math]}$ ，则 $\text{[math]}$ （）．

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九下·萧山月考) 已知二次函数 $\text{[math]}$ ，其中k ， m为常数，下列说法正确的是（）

A . 若 $\text{[math]}$ ，则二次函数y的最小值大于0 B . 若 $\text{[math]}$ ，则二次函数y的最小值小于0 C . 若 $\text{[math]}$ ，则二次函数y的最小值小于0 D . 若 $\text{[math]}$ ，则二次函数y的最小值大于0

答案解析收藏纠错 + 选题
10. (2024九下·萧山月考) 如图，边长为 $\text{[math]}$ 的小正方形网格中，点 $\text{[math]}$ 在格点上，连接 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上且满足 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题：本大题有6个小题，每小题3分，共18分.

11. (2024九下·秦安模拟) 分解因式： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2024·辽宁模拟) 一个不透明的袋中有若干个除颜色外完全相同的小球，其中黄球有6个，将袋中的球摇匀后，从中随机摸出一个球，记下它的颜色后再放回袋中，通过大量重复摸球试验后发现，摸到黄球的频率稳定在0.4左右，则袋中小球的个数为．

答案解析收藏纠错 + 选题
13. (2024九下·萧山月考) 如图，在⊙O中，AB切⊙O于点A，连接OB交⊙O于点C，过点A作AD∥OB交⊙O于点D，连接CD．若∠B=50°，则∠OCD的度数等于．

答案解析收藏纠错 + 选题
14. (2024八下·宁津月考) 已知 $\text{[math]}$ ， $\text{[math]}$ 是一次函数 $\text{[math]}$ 图像上不同的两点．若 $\text{[math]}$ ，则a的取值范围是．

答案解析收藏纠错 + 选题
15. (2024九下·萧山月考) 在Rt△ABC中，AC=BC ， ∠ACB=90°，P是CB延长线上的一点，BP：BC=k ，已知0≤k≤1，过点B作AB的垂线，过点P作AP的垂线，使两条垂线相交于点Q ，且AP=PQ ，连接AQ ，则△ABC与△APQ的面积比为（用k表示）.

答案解析收藏纠错 + 选题
16. (2024九下·萧山月考) 某校积极推行“互动生成的学本课堂”，九年级某学习小组在操作实践过程中发现了一个有趣的问题：将直尺和三角板（三角板足够大，直尺足够长）按如图所示的方式摆放在平面直角坐标系中，直尺的左侧边CD在直线x＝4上，在保证直角三角板其中一条直角边始终过点A（0，4），同时使得直角顶点E在直线CD上滑动，三角板的另一直角边与x轴交于点B ，则OB的最小值为．

答案解析收藏纠错 + 选题

三、解答题：本大题有8个小题，共72分. 解答应写出文字说明、证明过程或演算步骤.

17. (2024九下·萧山月考) 下面是小颖同学解一元一次方程的过程，请认真阅读并解答问题．
解方程： $\text{[math]}$
解：去分母，得 $\text{[math]}$ ……第一步
去括号，得 $\text{[math]}$ ……第二步
移项，得 $\text{[math]}$ ……第三步
合并同类项，得 $\text{[math]}$ ， ……第四步
方程两边同除以－1，得 $\text{[math]}$ ． ……第五步
1. （1）以上求解过程中，第三步的依据是____．
  
  A . 等式的基本性质 B . 不等式的基本性质 C . 分式的基本性质 D . 乘法分配律
2. （2）从第步开始出现错误；
3. （3）该方程正确的解为.
答案解析收藏纠错 + 选题
18. (2024九下·萧山月考) 某校学生会为了了解全校2000名学生对地震灾区的捐款情况，随机调查了部分学生的捐款金额，并用得到的数据绘制了如图统计图．
请根据相关信息，解答下列问题：
1. （1）本次接受随机抽样调查的学生人数为，图1中 $\text{[math]}$ %的值是%．
2. （2）求本次调查获取的样本数据的众数和中位数．
3. （3）根据样本数据，估算该校捐款金额为20元及以上的学生人数．
答案解析收藏纠错 + 选题
19. (2024九下·萧山月考) 已知反比例函数 $\text{[math]}$ 过点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ ， $\text{[math]}$ 时，求m的值：
2. （2）若 $\text{[math]}$ ，求n的值；
答案解析收藏纠错 + 选题
20. (2024九下·萧山月考) 已知：如图，在 $\text{[math]}$ 中， $\text{[math]}$ 于点 $\text{[math]}$ 是 $\text{[math]}$ 上一点，连结 $\text{[math]}$ ，已知 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ．
2. （2）若 $\text{[math]}$ 的面积为15，求的面积．
答案解析收藏纠错 + 选题
21. (2024·修水模拟) 图1为放在水平地面上的落地式话筒架实物图．图2为其示意图，支撑杆 $\text{[math]}$ 垂直于地面， $\text{[math]}$ ，斜杆 $\text{[math]}$ 连接在支撑杆顶端 $\text{[math]}$ 处， $\text{[math]}$ ，其中 $\text{[math]}$ 的长度可通过斜杆的滑动来进行调节，斜杆 $\text{[math]}$ 还可以绕着点 $\text{[math]}$ 旋转，且与支撑杆 $\text{[math]}$ 的夹角为 $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ 时，求话筒 $\text{[math]}$ 到地面的高度；
2. （2）落地式话筒可以根据使用者的身高需要调节 $\text{[math]}$ 的长度和夹角 $\text{[math]}$ 的度数，某运动员使用落地式话筒的适合高度是 $\text{[math]}$ ，请问该话筒的高度能否满足这名运动员的需要，并说明理由．（参考数据： $\text{[math]}$ ）
答案解析收藏纠错 + 选题
22. (2024八下·庐江期中) 如图，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，对角线 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是菱形；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长；
3. （3）在（2）的条件下，已知点M是线段 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．
答案解析收藏纠错 + 选题
23. (2024九下·萧山月考) 某课外科技活动小组研制了一种航模飞机．通过实验，收集了飞机相对于出发点的飞行水平距离 $\text{[math]}$ （单位： $\text{[math]}$ ）以、飞行高度 $\text{[math]}$ （单位： $\text{[math]}$ ）随飞行时间 $\text{[math]}$ （单位： $\text{[math]}$ ）变化的数据如下表．
飞行时间 $\text{[math]}$
0
2
4
6
8
…
飞行水平距离 $\text{[math]}$
0
10
20
30
40
…
飞行高度 $\text{[math]}$
0
22
40
54
64
…
1. （1）【探究发现】 $\text{[math]}$ 与 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系可以用我们已学过的函数来描述．
  任务一：直接写出 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式和 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式（不要求写出自变量的取值范围）．
2. （2）【问题解决】如图，活动小组在水平安全线上 $\text{[math]}$ 处设置一个高度可以变化的发射平台试飞该航模飞机．根据上面的探究发现解决下列问题．
  
  ①任务二：若发射平台相对于安全线的高度为0m，求飞机落到安全线时飞行的水平距离；
  ②任务三：在安全线上设置回收区域 $\text{[math]}$ ．若飞机落到 $\text{[math]}$ 内（不包括端点 $\text{[math]}$ ），求发射平台相对于安全线的高度的变化范围．
答案解析收藏纠错 + 选题
24. (2024九下·萧山月考) 如图，已知圆O是四边形 $\text{[math]}$ 的外接圆， $\text{[math]}$ 是直径．连接 $\text{[math]}$ 交 $\text{[math]}$ 于点E ．
1. （1）如图1，D是弧 $\text{[math]}$ 的中点，当 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；
2. （2）如图2， $\text{[math]}$ ，将 $\text{[math]}$ 绕点A顺时针旋转90°至 $\text{[math]}$ ，其中 $\text{[math]}$ 与 $\text{[math]}$ 重合，求证： $\text{[math]}$ ；
3. （3）如图3， $\text{[math]}$ ， F是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，过D点作 $\text{[math]}$ 交 $\text{[math]}$ 于点M ，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题