浙江省绍兴市第一初级中学2023-2024学年九年级下学期期...

更新时间：2024-12-13 浏览次数：9 类型：开学考试

一、选择题（本题有10小题,每小题3分,共30分）

1. (2024九下·绍兴开学考) $\text{[math]}$ 的相反数是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 3

答案解析收藏纠错 + 选题
2. (2024九下·绍兴开学考) 2023年9月23日，第19届亚运会在杭州开幕，开幕式现场直播及相关报道在多媒体平台的总播放量约为503000000次，其中数据“503000000”用科学记数法表示为（）

A . 50.3×10⁷ B . 5.03×10⁸ C . 50.3×10⁸ D . 5.03×10⁹

答案解析收藏纠错 + 选题
3. (2024九下·绍兴开学考) 下列计算正确的是（　　）

A . a²+a⁴＝a⁶ B . （﹣a³）²＝a⁶ C . 2a+3b＝5ab D . a⁶÷a³＝a²

答案解析收藏纠错 + 选题
4. (2024九下·兰陵模拟) 如图所示放置的正三棱柱的俯视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024九下·绍兴开学考) 已知点P关于x轴对称的点的坐标为（﹣1，2），则点P的坐标为（　　）

A . （2，1） B . （1，﹣2） C . （1，2） D . （﹣1，﹣2）

答案解析收藏纠错 + 选题
6. (2024七下·成都期末) 我国古代《算法统宗》里有这样一首诗：“我问开店李三公，众客都来到店中，一房七客多六客，一房八客一房空．”诗中后面两句的意思是：如果一间客房住7人，那么有6人无房可住；如果一间客房住8人，那么就空出一间客房，若设该店有客房x间，房客y人，则列出关于x、y的二元一次方程组正确的是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·绍兴开学考) “少年强则国强；强国有我，请党放心．”这句话中，“强”字出现的频率是（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
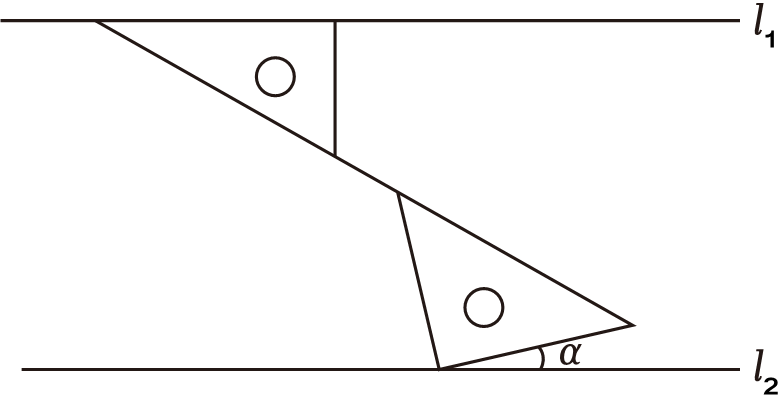
8. (2024九下·绍兴开学考) 如图，直线l₁∥l₂ ，一副三角板放置在l₁ ， l₂之间，一三角板直角边在l₁上，三角板斜边在同一直线上，则∠α＝（　　）

A . 10° B . 15° C . 20° D . 25°

答案解析收藏纠错 + 选题
9. (2024九下·绍兴开学考) 摄影中有一种拍摄手法叫黄金构图法．其原理是：如图，在正方形ABCD的底边BC取中点E，以E为圆心，线段DE长为半径作圆，与底边BC的延长线交于点F，矩形ABFG称为黄金矩形．若CF＝4，则AB为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024九下·绍兴开学考) 如图，反比例函数 $\text{[math]}$ 的图象与矩形OABC的边AB、BC分别相交于点D、E，连接OD、OE，直线DE与x轴、y轴分别相交于点M、N，则下列结论正确的是（　　）
①S_△_OCE＝S_△_OAD； ② $\text{[math]}$ ；③DM＝EN；④若S_△_ODE＝9.6，S_长方形_OABC＝20，则k＝4．

A . ①② B . ①②③ C . ②③④ D . ①②③④

答案解析收藏纠错 + 选题

二、填空题（本题有6小题,每小题4分,共24分）

11. (2024九下·绍兴开学考) 要使分式 $\text{[math]}$ 有意义，则x应满足的条件是．

答案解析收藏纠错 + 选题
12. (2024九下·绍兴开学考) 分解因式8x³y﹣18xy＝．

答案解析收藏纠错 + 选题
13. (2024九下·绍兴开学考) 直线y＝k₂x和y＝k₁x+b如图所示，则关于x的不等式k₂（x﹣2）＜k₁（x﹣2）+b的解集是．

答案解析收藏纠错 + 选题
14. (2024九下·绍兴开学考) 如图，AB是⊙O的弦，OA，OB是⊙O的半径，∠A＝20°，若C是⊙O上异于A，B两点的另一点，则∠ACB的度数是．

答案解析收藏纠错 + 选题
15. (2024九下·绍兴开学考) 如图1，一个扇形纸片的圆心角为90°，半径为10．如图2，将这张扇形纸片折叠，使点A与点O恰好重合，折痕为CD，图中阴影为重合部分，则阴影部分的面积为．（结果保留π）

答案解析收藏纠错 + 选题
16. (2024九下·绍兴开学考) 如图1是七巧板图案，现将它剪拼成一个“台灯”造型（如图2），过该造型的上下左侧五点作矩形ABCD，使得 $\text{[math]}$ ，点N为PQ的中点，并且在矩形内右上角部分留出正方形EFGH作为印章区域（EH∥AD，HG∥CD），形成一幅装饰画，则矩形ABCD的周长为cm．若点M，N，E在同一直线上，且点H到AD的距离与到CD的距离相等，则印章区域的面积为cm² ．

答案解析收藏纠错 + 选题

三、解答题（本题有8小题,第17～19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分,各小题都必须写出解答过程）

17. (2024九下·绍兴开学考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2024九下·绍兴开学考) 解不等式组 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2024九下·绍兴开学考) 如图，在平面直角坐标系中，已知△ABC的三个顶点都在格点上，坐标分别为A（2，4），B（1，2），C（5，3）．
1. （1）画出△ABC关于原点O对称的△A₁B₁C₁；
2. （2）画出△ABC绕原点O顺时针旋转90°的△A₂B₂C₂ ，写出B₂点坐标．
3. （3）在x轴上找一点P，使PB+PC的和最小，求出P点坐标．
答案解析收藏纠错 + 选题
20. (2024九下·绍兴开学考) 学习习近平总书记关于生态文明建设重要讲话，牢固树立“绿水青山就是金山银山”的科学观，让环保理念深入到学校.某校张老师为了了解本班学生3月植树成活情况，对本班全体学生进行了调查，并将调查结果分为三类：A：好，B：中， $\text{[math]}$ ：差.请根据图中信息，解答下列问题：
1. （1）求全班学生总人数；
2. （2）在扇形统计图中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 类的圆心角为；
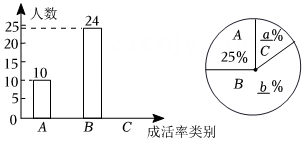
3. （3）张老师在班上随机抽取了4名学生，其中 $\text{[math]}$ 类1人， $\text{[math]}$ 类2人， $\text{[math]}$ 类1人，若再从这4人中随机抽取2人，请用列表法或画树状图的方法求出全是 $\text{[math]}$ 类学生的概率.
答案解析收藏纠错 + 选题
21. (2024九下·绍兴开学考) 如图，已知斜坡AB长为60米，坡角（即∠BAC）为30°，BC⊥AC，现计划在斜坡中点D处挖去部分坡体（用阴影表示），修建一个平行于水平线CA的平台DE和一条新的斜坡BE．
1. （1）若修建的斜坡BE的坡角为45°，求平台DE的长；（结果保留根号）
2. （2）一座建筑物GH距离A处30米远（即AG为30米），小明在D处测得建筑物顶部H的仰角（即∠HDM）为30°，点B、C、A、G、H在同一个平面内，点C、A、G在同一条直线上，且HG⊥CG，求建筑物GH的高度．（结果保留根号）
答案解析收藏纠错 + 选题
22. (2024九下·绍兴开学考) 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是边 $\text{[math]}$ 上的一点（不与 $\text{[math]}$ 、 $\text{[math]}$ 重合）， $\text{[math]}$ ，垂足为 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
23. (2024九下·绍兴开学考) 已知点（﹣m，0）和（3m，0）在二次函数y＝ax²+bx+3（a，b是常数，a≠0）的图象上．
1. （1）当m＝2时，求a和b的值；
2. （2）若二次函数的图象经过点A（﹣n，3）且点A不在坐标轴上，当﹣2＜m＜1时，求n的取值范围；
3. （3）求证：b²+4a＝0．
答案解析收藏纠错 + 选题
24. (2024九下·绍兴开学考) 如图1，在圆内接四边形ABCD中，AD，BC的延长线交于点E，连结BO并延长交AD于点G，连结BD．已知BD＝AB，∠CDE＝3∠CBD， $\text{[math]}$ ， BO＝5．
图1 图2
1. （1）求证：∠GBD＝∠CBD．
2. （2）求OG与GD的长．
3. （3）如图2，F是BO中点，动点P在FG上从点F向终点G匀速运动，同时动点Q在AE上从点E向终点A匀速运动．当点Q在点D处时，点P在点O处，设QE＝x，PG＝y．
  ①求y关于x的表达式．
  ②连结PQ，当直线PQ与△BCD的某一边所在的直线垂直时，记垂足为点M，直接写出QM的值．
答案解析收藏纠错 + 选题