题库组卷系统-专注K12在线组卷服务

在线咨询

当前：高中数学

当前位置：高中数学 /备考专区

试卷结构：课后作业日常测验标准考试

| 显示答案解析 | 全部加入试题篮 | 平行组卷试卷细目表发布测评在线自测试卷分析收藏试卷试卷分享

下载试卷下载答题卡

四川省眉山市东坡区多悦高级中学校2023-2024学年高一下...

更新时间：2024-04-29 浏览次数：30 类型：期中考试

一、选择题（本题共8道小题，每小题5分，共40分）

1. (2024高一下·东坡期中) cos(－510°)=（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高一下·东坡期中) $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高一下·东坡期中) 已知 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . -2 D . 2

答案解析收藏纠错 + 选题
4. (2024高一下·东坡期中) 已知角 $\text{[math]}$ 的终边经过点 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高一下·东坡期中) 已知 $\text{[math]}$ ，则 $\text{[math]}$

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高一下·东坡期中) 若函数 $\text{[math]}$ 同时满足下列三个性质：①最小正周期为 $\text{[math]}$ ；②图象关于直线 $\text{[math]}$ 对称；③在区间 $\text{[math]}$ 上是增函数，则 $\text{[math]}$ 的解析式可以是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高一下·东坡期中) 要得到 $\text{[math]}$ 的图像，只需将函数 $\text{[math]}$ 的图像（）

A . 向左平移 $\text{[math]}$ 个单位 B . 向右平移 $\text{[math]}$ 个单位 C . 向左平移 $\text{[math]}$ 个单位 D . 向右平移 $\text{[math]}$ 个单位

答案解析收藏纠错 + 选题
8. (2024高一下·东坡期中) 将函数 $\text{[math]}$ 的图像向右平移 $\text{[math]}$ 个长度单位后，所得到的图像关于 $\text{[math]}$ 轴对称，则 $\text{[math]}$ 的最小值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题（本题共3道小题，每小题6分，共18分）

9. (2024高一下·东坡期中) 下列四个函数中，以 $\text{[math]}$ 为最小正周期，且在区间 $\text{[math]}$ 上单调递减的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024高一下·东坡期中) 已知 $\text{[math]}$ ，下列说法正确的有（）

A . $\text{[math]}$ 的最小正周期是 $\text{[math]}$ B . $\text{[math]}$ 最大值为2 C . $\text{[math]}$ 的图象关于 $\text{[math]}$ 对称 D . $\text{[math]}$ 的图象关于 $\text{[math]}$ 对称

答案解析收藏纠错 + 选题
11. (2024高一下·东坡期中) 已知 $\text{[math]}$ （其中 $\text{[math]}$ ， $\text{[math]}$ ）的部分图像如图所示，则下列说法正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 函数 $\text{[math]}$ 在区间 $\text{[math]}$ 单调递减 D . 若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题（本题共3道小题，每小题5分，共15分）

12. (2024高一下·东坡期中) $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
13. (2024高一下·东坡期中) 化简 $\text{[math]}$

答案解析收藏纠错 + 选题
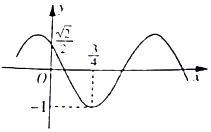
14. (2024高一下·东坡期中) 已知函数f(x)=sin(ωx+φ)( ω＞0， φ∈( $\text{[math]}$ ， π))的部分图象如图所示，则f（2021）＝．

答案解析收藏纠错 + 选题

四、解答题（本题共5道小题,第1题13分,第2题15分,第3题15分,第4题17分,第5题17分,共77分）

15. (2024高一下·东坡期中) 已知 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ 的值；
2. （2）求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
16. (2024高一下·东坡期中) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$
1. （1）求 $\text{[math]}$ 的值；
2. （2）求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
17. (2024高一下·东坡期中) 已知函数 $\text{[math]}$ .
1. （1）求函数 $\text{[math]}$ 的单调递增区间；
2. （2）若函数 $\text{[math]}$ 的图像关于点 $\text{[math]}$ 中心对称，求 $\text{[math]}$ 在 $\text{[math]}$ 上的值域.
答案解析收藏纠错 + 选题
18. (2024高一下·东坡期中) 已知函数 $\text{[math]}$ ．
1. （1）求函数f(x)的最大值；
2. （2）把 $\text{[math]}$ 的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把得到的图象向左平移 $\text{[math]}$ 个单位，得到函数 $\text{[math]}$ 的图象，求函数 $\text{[math]}$ 的单调递减区间
答案解析收藏纠错 + 选题
19. (2024高一下·东坡期中) 某游乐场的摩天轮示意图如图．已知该摩天轮的半径为30米，轮上最低点与地面的距离为2米，沿逆时针方向匀速旋转，旋转一周所需时间为 $\text{[math]}$ 分钟．在圆周上均匀分布12个座舱，标号分别为1~12（可视为点），在旋转过程中，座舱与地面的距离h与时间t的函数关系基本符合正弦函数模型，现从图示位置，即1号座舱位于圆周最右端时开始计时，旋转时间为t分钟．
1. （1）求1号座舱与地面的距离h与时间t的函数关系 $\text{[math]}$ 的解析式；
2. （2）在前24分钟内，求1号座舱与地面的距离为17米时t的值；
3. （3）记1号座舱与5号座舱高度之差的绝对值为H米，求当H取得最大值时t的值．
答案解析收藏纠错 + 选题

试卷信息