四川省德阳市第二中学校2023-2024学年八年级下学期4月...

更新时间：2024-07-30 浏览次数：8 类型：月考试卷

一、单选题（本题共12个小题，每小题4分，共48分，每个小题只有一个正确选项）

1. (2024八下·确山期末) 下列各式中，正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·德阳月考) 已知，如图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距（）

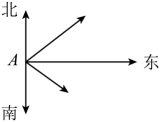
A . 25海里 B . 30海里 C . 35海里 D . 40海里

答案解析收藏纠错 + 选题
3. (2024八下·凉州期中) 下列二次根式中，不能与 $\text{[math]}$ 合并的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·德阳月考) 能判断 $\text{[math]}$ 是直角三角形的是（）

A . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九上·重庆市开学考) 估计 $\text{[math]}$ 的值应在（）

A . 10和11之间 B . 9和10之间 C . 8和9之间 D . 7和8之间

答案解析收藏纠错 + 选题
6. (2024八下·德阳月考) 如图，在等腰 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点A ， B分别在x轴，y轴上，且 $\text{[math]}$ 轴，将 $\text{[math]}$ 沿x轴向左平移，当点A与点O重合时，点B的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024八下·临沂月考) 若 $\text{[math]}$ ， $\text{[math]}$ ，则a与b的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 不能确定

答案解析收藏纠错 + 选题
8. (2024八下·德阳月考) 如图， $\text{[math]}$ 是四根长度均为5的火柴棒，均位于一条不完整的数轴上方．若点 $\text{[math]}$ 、点 $\text{[math]}$ 分别对应实数 $\text{[math]}$ ，且 $\text{[math]}$ ，则点 $\text{[math]}$ 所对应的实数为（）

A . 8 B . 9 C . 10 D . 11

答案解析收藏纠错 + 选题
9. (2024八下·德阳月考) 化简二次根式 $\text{[math]}$ 的结果是（）

A . $\text{[math]}$ B . － $\text{[math]}$ C . $\text{[math]}$ D . － $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024八下·德阳月考) 有一题目：“在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ． ”嘉嘉的解答为：画 $\text{[math]}$ ，截取 $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于 $\text{[math]}$ ，如图，由于 $\text{[math]}$ ，易得 $\text{[math]}$ ，在 $\text{[math]}$ 中， $\text{[math]}$ ，由勾股定理可得 $\text{[math]}$ ，得 $\text{[math]}$ ，而淇淇说：“嘉嘉考虑的不周全， $\text{[math]}$ 还应有另一个不同的值．”下列判断正确的是（）

A . 淇淇说的不对， $\text{[math]}$ 就得 $\text{[math]}$ B . 嘉嘉的结果不对， $\text{[math]}$ 不是 $\text{[math]}$ C . 淇淇说的对， $\text{[math]}$ 的另一个值是 $\text{[math]}$ D . 两人都不对， $\text{[math]}$ 应有 $\text{[math]}$ 个不同值

答案解析收藏纠错 + 选题
11. (2024八下·德阳月考) 若a、b、c为有理数，且等式 $\text{[math]}$ 成立，则2a＋999b＋1001c的值是（）

A . 1999 B . 2000 C . 2001 D . 不能确定

答案解析收藏纠错 + 选题
12. (2024八下·德阳月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D、E为 $\text{[math]}$ 上两点， $\text{[math]}$ ， F为 $\text{[math]}$ 外一点，且 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论： $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ，其中正确的是（）

A . ①②③ B . ①②③④ C . ①③④ D . ②③

答案解析收藏纠错 + 选题

二、填空题（本大题共7小题，每小题4分，共28分）

13. (2024八下·德阳月考) 如果代数式 $\text{[math]}$ 有意义，那么x的取值范围是.

答案解析收藏纠错 + 选题
14. (2024七下·苏州月考) 命题“如果 $\text{[math]}$ ，那么 $\text{[math]}$ ”，则它的逆命题是命题（填“真”或“假”）．

答案解析收藏纠错 + 选题
15. (2024八下·德阳月考) 如图，在数轴上，以单位长度为边长画正方形，以正方形对角线长为半径画弧，与数轴交于点 $\text{[math]}$ ，则点 $\text{[math]}$ 表示的数为．

答案解析收藏纠错 + 选题
16. (2024八下·德阳月考) 有理数 $\text{[math]}$ 在数轴上对应点的位置如图所示，化简： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
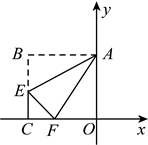
17. (2024八下·德阳月考) 如图，在平面直角坐标系中，长方形 $\text{[math]}$ 的边 $\text{[math]}$ 分别在 $\text{[math]}$ 轴、 $\text{[math]}$ 轴上， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，将长方形 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，若点 $\text{[math]}$ 的对应点 $\text{[math]}$ 恰好是边 $\text{[math]}$ 的三等分点，则点 $\text{[math]}$ 的坐标是．

答案解析收藏纠错 + 选题
18. (2024八下·德阳月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，以 $\text{[math]}$ 的各边为边作三个正方形，点 $\text{[math]}$ 落在 $\text{[math]}$ 上，若 $\text{[math]}$ ，空白部分面积为10，则 $\text{[math]}$ 的长．

答案解析收藏纠错 + 选题
19. (2024八下·德阳月考) 人们把 $\text{[math]}$ 这个数叫做黄金分割数，著名数学家华罗庚优选法中的 $\text{[math]}$ 法就应用了黄金分割数．设 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ，记 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

三、解答题（本大题共6小题，共74分，解答应写过程）

20. (2024八下·德阳月考) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ；
3. （3） $\text{[math]}$ ；
4. （4） $\text{[math]}$ ；
5. （5）当 $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的值；
6. （6）已知x ， y是实数，且满足 $\text{[math]}$ ，化简： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2024八下·德阳月考) 定义： $\text{[math]}$ 为正整数，若 $\text{[math]}$ ，则称 $\text{[math]}$ 为“完美勾股数”， $\text{[math]}$ 为 $\text{[math]}$ 的“伴侣勾股数”．如 $\text{[math]}$ ，则13是“完美勾股数”，5，12是13的“伴侣勾股数”．
1. （1）数10“完美勾股数”（填“是”或“不是”）；
2. （2）已知 $\text{[math]}$ 的三边 $\text{[math]}$ 满足 $\text{[math]}$ ．求证： $\text{[math]}$ 是“完美勾股数”．
答案解析收藏纠错 + 选题
22. (2024八下·德阳月考) 数学张老师在课堂上提出一个问题：“通过探究知道： $\text{[math]}$ ，它是个无限不循环小数，也叫无理数，它的整数部分是1，那么有谁能说出它的小数部分是多少”，小明举手回答：它的小数部分我们无法全部写出来，但可以用 $\text{[math]}$ 来表示它的小数部分，张老师夸奖小明真聪明，肯定了他的说法．现请你根据小明的说法解答：
1. （1） $\text{[math]}$ 的整数部分是．
2. （2） $\text{[math]}$ 为 $\text{[math]}$ 的小数部分， $\text{[math]}$ 为 $\text{[math]}$ 的整数部分，求 $\text{[math]}$ 的值．
3. （3）已知 $\text{[math]}$ ，其中 $\text{[math]}$ 是一个正整数， $\text{[math]}$ ，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
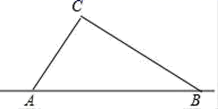
23. (2024八下·德阳月考) 森林火灾是一种常见的自然灾害，危害很大，随着中国科技、经济的不断发展，开始应用飞机洒水的方式扑灭火源.如图，有一台救火飞机沿东西方向AB，由点A飞向点B，已知点C为其中一个着火点，且点 C与直线 AB上两点A，B的距离分别为600m和800m，又AB＝1000m，飞机中心周围500m 以内可以受到洒水影响.
1. （1）着火点C受洒水影响吗？为什么？
2. （2）若飞机的速度为10 m/s，要想扑灭着火点C估计需要13秒，请你通过计算判断着火点C能否被扑灭？
答案解析收藏纠错 + 选题
24. (2024八下·德阳月考) 如图，在 $\text{[math]}$ 中，过点A作 $\text{[math]}$ ，交 $\text{[math]}$ 于点D ．
1. （1）若 $\text{[math]}$ ，求 $\text{[math]}$ 的长；
2. （2）在（1）的条件下， $\text{[math]}$ ，求 $\text{[math]}$ 的面积；
3. （3）若 $\text{[math]}$ ，求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
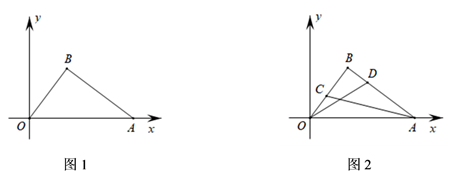
25. (2024八下·德阳月考) 如图1，在平面直角坐标系xOy中，点A的坐标为（5，0），点B在第一象限内，且使得AB = 4，OB = 3．
1. （1）试判断△AOB的形状，并说明理由；
2. （2）在第二象限内是否存在一点P，使得△POB是以OB为腰的等腰直角三角形，若存在，求出点P的坐标：若不存在，请说明理由；
3. （3）如图2，点C为线段OB上一动点，点D为线段BA上一动点，且始终满足OC = BD．求AC + OD的最小值．
答案解析收藏纠错 + 选题