广东省深圳市龙华区民治中学2023-2024学年七年级下学期...

更新时间：2024-05-10 浏览次数：17 类型：期中考试

一、选择题：本大题共10小题，每小题3分，共30分。每小题只有一个选项符合题目要求。

1. (2024七下·深圳期中) $\text{[math]}$ 的余角是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024七下·深圳期中) 1986年9月，深圳市评选簕杜鹃为深圳市市花，簕杜鹃又名三角梅、九重葛。簕杜鹃属于紫茉莉科叶子花属的藤状灌木，具有旺盛的生命力和较长的花期，它的苞片大而美丽，颜色鲜艳，给人以奔放、热烈的感受。簕杜鹃的单粒的花粉粒直径约为 $\text{[math]}$ ，数据0.000015用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024七下·深圳期中) 如图，我们把剪刀的两边抽象成两条相交的直线，若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·深圳期末) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024七下·五华期中) 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 3 B . 4 C . 12 D . 36

答案解析收藏纠错 + 选题
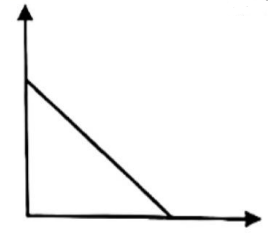
6. (2024七下·深圳期中) 如图，点 $\text{[math]}$ 处安装了一个路灯，能照射范围的水平距离为线段 $\text{[math]}$ ，测得 $\text{[math]}$ ， $\text{[math]}$ ，则点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离可能为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024七下·深圳期中) 下列实际情境中的变量关系可以用如图近似地刻画的是（）

A . 匀速骑行的自行车（速度与时间的关系） B . 篮球运动员投出去的篮球（高度与时间的关系） C . 燃烧的蜡烛（蜡烛长度与时间的关系） D . 早晨升旗仪式（国旗高度与时间的关系）

答案解析收藏纠错 + 选题
8. (2024七下·深圳期中) 如图，已知直线 $\text{[math]}$ ，现将含 $\text{[math]}$ 角的直角三角板放入平行线之间，两个锐角顶点分别落在两条直线上．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024七下·深圳期末) 多项式 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 6 B . $\text{[math]}$ C . 8 D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024七下·深圳期中) 如图，在长方形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，对角线 $\text{[math]}$ ，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿 $\text{[math]}$ 运动．设点 $\text{[math]}$ 的运动路程为 $\text{[math]}$ ， $\text{[math]}$ 的面积为 $\text{[math]}$ ．若 $\text{[math]}$ 与 $\text{[math]}$ 的对应关系如图所示．则图中 $\text{[math]}$ （）

A . $\text{[math]}$ B . 1 C . 3 D . 4

答案解析收藏纠错 + 选题

二、填空题（本大题共5小题，每小题3分，共15分）

11. (2024七下·深圳期中) $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2024七下·深圳期中) 随着气温下降，人们开始增添衣服，在这个问题中，自变量是．

答案解析收藏纠错 + 选题
13. (2024七下·深圳期中) 若 $\text{[math]}$ 是一个完全平方式，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024七下·深圳期中) 如图， $\text{[math]}$ 的两边被一张长方形纸片部分遮挡．若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
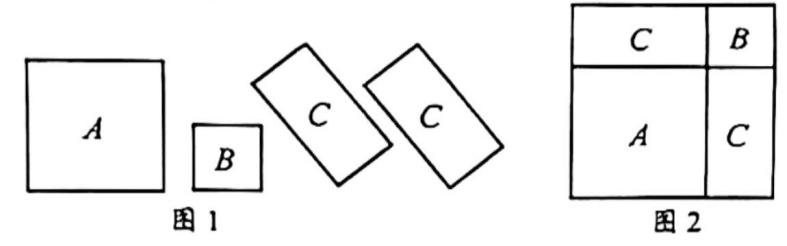
15. (2024七下·深圳期中) 七巧板起源于我国先秦时期，古算书《周髀算经》中有关于正方形的分割术，经过历代演变而成七巧板．小深先用一副七巧板拼成了图1，图1的轮廓是一个边长为 $\text{[math]}$ 的正方形，其中 $\text{[math]}$ ，小等腰直角三角板 $\text{[math]}$ 的面积为 $\text{[math]}$ ，小深拿掉七巧板中的一块，又将剩下的六块拼成一个新的图形，其轮廓和 $\text{[math]}$ 板的位置如图2所示，则图2的面积为．

答案解析收藏纠错 + 选题

三、解答题：本题共7小题，共55分．解答应写出文字说明、证明过程或演算步骤．

16. (2024七下·深圳期中) 计算： $\text{[math]}$ ；

答案解析收藏纠错 + 选题
17. (2024七下·深圳期中) 小深在对多项式 $\text{[math]}$ “化简求值”的过程中，发现只需要知道字母 ▲ （填 $\text{[math]}$ 或 $\text{[math]}$ ）的取值就可以求出正确答案了，若这个字母等于3，请将这个多项式先化简，再求值．

答案解析收藏纠错 + 选题
18. (2024七下·深圳期中) 如图1，点 $\text{[math]}$ 为 $\text{[math]}$ 边 $\text{[math]}$ 上一点，
1. （1）利用直尺和圆规：过点 $\text{[math]}$ 作直线 $\text{[math]}$ ，使 $\text{[math]}$ ．（用黑色水笔描出作图痕迹，不要求写作法）
2. （2）如图2，在（1）的前提下， $\text{[math]}$ 为 $\text{[math]}$ 上一点，过 $\text{[math]}$ 作 $\text{[math]}$ ，求证： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2024七下·深圳期中) 某新型品牌充电器给手机充电时充电速度是匀速的，一台手机屏幕画面显示初始电量为 $\text{[math]}$ ，其电量 $\text{[math]}$ （单位： $\text{[math]}$ ）与充电时间 $\text{[math]}$ （单位：h）为表格中几组对应值．根据以上信息，回答下列问题：
充电时间 $\text{[math]}$ （单位：h）
0
0.25
0.5
$\text{[math]}$
1.5
电量 $\text{[math]}$ （单位： $\text{[math]}$ ）
20
$\text{[math]}$
40
60
80
1. （1） $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）该手机充电直至电量达到 $\text{[math]}$ 需要多久？
答案解析收藏纠错 + 选题
20. (2024七下·深圳期中) 如图，正方形纸板 $\text{[math]}$ 的边长为 $\text{[math]}$ ，正方形纸板 $\text{[math]}$ 的边长为 $\text{[math]}$ ，用一块纸板 $\text{[math]}$ 、一块纸板 $\text{[math]}$ 和两块长方形纸板 $\text{[math]}$ 可以拼成一个大正方形．
1. （1）图2大正方形的边长为；由图1到图2，可以得到一个关于 $\text{[math]}$ 的等式，直接写出这个等式：；
2. （2）利用这个等式解决如下问题：长方形纸板 $\text{[math]}$ 的周长为12，正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ 的面积之和为26，求长方形纸板 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
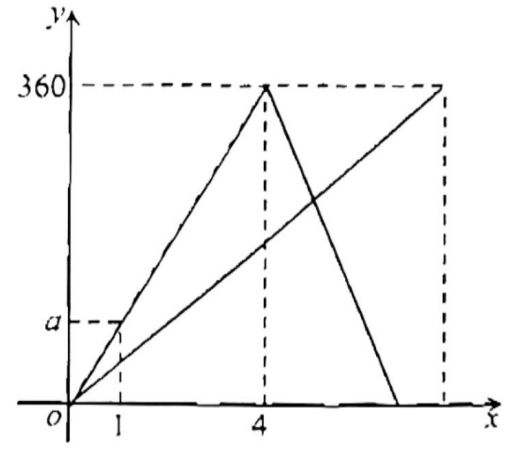
21. (2024七下·深圳期中) 已知甲乙两地相距 $\text{[math]}$ ，一辆轿车从甲地出发往返于甲乙两地，一辆货车匀速沿同一条路线从乙地前往甲地，两车同时出发，经过 $\text{[math]}$ 后两车第一次相遇．轿车到达乙地后立即按原路返回，结果比货车早一个小时到达甲地．如图是两车距各自出发地的距离 $\text{[math]}$ 与货车行驶时间 $\text{[math]}$ 之间的函数图象，结合图象回答下列问题：
1. （1）图中 $\text{[math]}$ 的值是；
2. （2）求轿车到达乙地再返回甲地所花费的时间；
3. （3）轿车在返回甲地的过程中与货车相距 $\text{[math]}$ ，直接写出货车已经从乙地出发了多长时间？
答案解析收藏纠错 + 选题
22. (2024七下·深圳期中) 【问题背景】光线照射到镜面会产生反射现象，小圳在做镜面反射实验时发现：当光线经过镜面反射时，入射光线、反射光线与镜面所夹的角对应相等．例如：在图1中，有 $\text{[math]}$ ．
1. （1）【初步探究】如图2，设镜子AB与BC的夹角 $\text{[math]}$ ，当 $\text{[math]}$ 时，小圳发现入射光线EF与反射光线GH恰好平行．
2. （2）【深入探究】如图3，小圳渐渐改变两镜面之间夹角，使得 $\text{[math]}$ 是一个锐角，从F点发出一条光线EF经过2次反射又回到了点F ，入射光线EF与第2次反射光线GF的夹角为 $\text{[math]}$ ．用含 $\text{[math]}$ 的式子表示 $\text{[math]}$ ．
3. （3）【拓展应用】如图4，小圳继续改变两镜面之间夹角，使得 $\text{[math]}$ ，若 $\text{[math]}$ 也是一个钝角，入射光线EF与镜面AB的夹角 $\text{[math]}$ ．已知入射光线EF从镜面AB开始反射，经过3次反射，当第3次反射光线与入射光线EF平行时，求出 $\text{[math]}$ 的度数．
答案解析收藏纠错 + 选题