

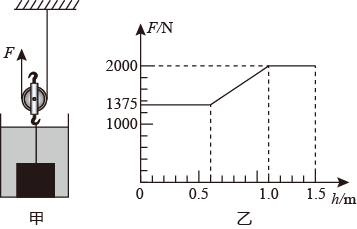






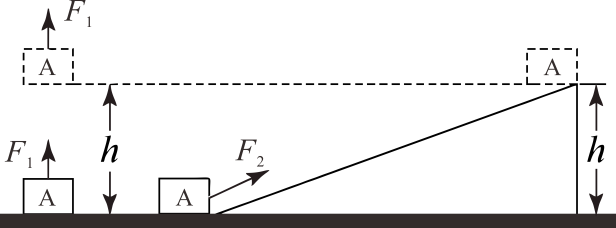
①一定大于
②甲的额外功一定等于乙的额外功
③若重物的重力相同,则甲的机械效率小于乙的机械效率
④若做功的功率大于
做功的功率,则甲的机械效率大于乙的机械效率






|
实验次数 |
钩码所受的重力G/N |
钩码上升的高度h/cm |
拉力F/N |
绳自由端移动的距离s/cm |
机械效率η |
|
1 |
2 |
10 |
0.8 |
30 |
83.3% |
|
2 |
4 |
10 |
1.5 |
30 |
② |
|
3 |
6 |
10 |
① |
30 |
* |
某实验小组在测滑轮组机械效率的实验中得到的数据如表所示,实验装置如图所示.

实验次数 | 1 | 2 | 3 |
钩码重G/N | 4 | 4 | 6 |
钩码上升高度h/m | 0.1 | 0.1 | 0.1 |
绳端拉力F/N | 1.8 | 1.6 | 1.8 |
绳端移动距离s/m | 0.3 | 0.4 | |
机械效率η | 74.1% | 62.5% |

|
实验 次数 |
滑轮 材质 |
钩码重 G/N |
提升的高度 h/m |
有用功 W有用/J |
拉力 F/N |
绳端移动的距离 S/m |
总功 W总/J |
机械效率 η |
|
1 |
铝 |
1 |
0.1 |
0.1 |
0.6 |
0.3 |
0.18 |
56% |
|
2 |
铝 |
2 |
0.1 |
0.2 |
1.0 |
0.3 |
0.3 |
67% |
|
3 |
铝 |
2 |
0.2 |
0.4 |
1.0 |
0.6 |
0.6 |
67% |
|
4 |
塑料 |
2 |
0.2 |
0.4 |
0.8 |
0.6 |
0.48 |
83% |
|
5 |
塑料 |
2 |
0.2 |
0.4 |
2.1 |
0.2 |
0.42 |
95% |
①比较1和2两次实验发现:在所有滑轮组一定时,提升的钩码,机械效率越高。
②比较3和4两次实验发现:滑轮组的机械效率还与有关。
③比较两次实验发现:在所用滑轮组一定时,机械效率与提升钩码的高度无关。
④第5次实验是利用了图的装置完成的,判断依据是。
⑤利用图甲的装置,把重6N的物体用2.5N的拉力迅速拉起,滑轮组的机械效率为。可见如果没有刻度尺,只有测力计,也可以测量出滑轮组的机械效率。
A、焦耳定律 B、牛顿第一定律 C、阿基米德原理 D、欧姆定律
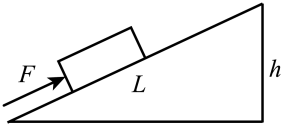
A.斜面的机械效率可能与物体的重力有关.
B.斜面的机械效率可能与斜面的倾斜程度有关.
小华同学为了证实自己的猜想是否正确,于是他用同一块木板组成如图所示的装置进行了实验探究,记录的实验数据如下表:

实验 次数 | 斜面倾角θ | 物块重量 G/N | 斜面高度 h/m | 沿斜面拉力F/N | 斜面长 S/m | 有用功 W有/J | 总 功 W总/J | 斜面的机械效率 |
1 | 30° | 5.0 | 0.6 | 4.2 | 1.2 | 3.0 | 5.0 | |
2 | 30° | 3.0 | 0.6 | 2.5 | 1.2 | 1.8 | 60% | |
3 | 45° | 3.0 | 0.8 | 2.8 | 1.2 | 2.4 | 3.4 | 71% |
![]()


小海设计了一种用力传感器感知抽水量的长方体水舱模型,其底面积为2m2 , 示意图如图丙所示,其中A是固定的力传感器,能够显示B对它的压力或拉力的大小;B是质量和体积均可忽略的细直杆,B的上端固定在A上,下端固定在物体C上;物体C是质量为20kg、高度为2m的圆柱体。水舱中装有4.2m3的水,抽水机将水抽出的过程中,力传感器示数F的大小随抽出水的体积V变化的图象如图丁所示。当力传感器示数为0时,剩余的水对舱底的压强是多少?


①若底部支撑台与地面接触面积为0.04m2 , 顶起汽车车身后手不再用力,则千斤顶对地面产生的压强是多大?
②顶起汽车车身后,为了方便更换轮胎,需要继续摇动扳手,使顶升继续升高一段距离,若人摇动扳手使顶升在1min内升高12cm,用千斤顶顶起车身时的机械效率为80%,则人做功的功率是多大?