一、选择题(本大题共16个小题,共38分.1~6小题各3分,7~16小题各2分在每小题给出的四个选项中,只有一项是符合题目要求的)
-
A . -2
B . 2
C .  D .
D . 
-
2.
(2024·海港模拟)
如图,嘉琪同学的家在

处,书店在

处,星期日她到书店去买书,想尽快赶到书店,请你帮助她选择一条最近的路线是( )

-
-
4.
(2024·海港模拟)
5纳米芯片非常小,相比之下,人类头发的直径大约为100000纳米,即5纳米只有人类头发直径的

用科学记数法表示为( )
-
A . 3米
B . 6.5米
C . 9米
D . 15米
-
6.
(2024·海港模拟)
幂的乘方运算、法则推导过程如下:
 (第一步)
(第一步)
 (第二步)
(第二步)
 (第三步)
(第三步)
甲:第一步的依据是乘方的意义;乙:第二步的依据是问底数幂的乘法法则;
丙:第三步的依据是乘法的意义.下列判断正确的是:( )
A . 甲、乙、丙都对
B . 甲、乙,丙都错
C . 只有丙错
D . 只有乙错
-
-
-
9.
(2024·海港模拟)
如图1,锐角

中,

为
BC边上一点(不与
B、C重合),连接
AD.在
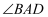
、

三个角中,某两个角之间的关系图像如图2.下列说法:①纵轴

表示
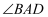
, 横轴

表示

;
② ③
③ , 正确的是( )
, 正确的是( )

A . ①③
B . ③
C . ②③
D . ①②③
-
A . 段①
B . 段②
C . 段③
D . 段④
-
A . 只有①
B . 只有②
C . ①②
D . ①②③
-
12.
(2024·海港模拟)
在

中,只用无刻度直尺和圆规比较

与

的大小.除了“叠合法”外,嘉琪又想出两种方法:( )
方法一:作 的高AD和角平分线AE , 若
的高AD和角平分线AE , 若 点在线段BD上,则说明
点在线段BD上,则说明 .
.
方法二:作BC边中垂线MN,若MN与AB边相交(不包括A点),则说明
A . 方法一可行,方法二不可行
B . 方法二可行,方法一不可行
C . 两种方法都可行
D . 两种方法都不可行
-
13.
(2024·海港模拟)
如图,

, 以

为原点,向右为正方向,

为1个单位长度建立数轴.点

表示数

, 则

与

的函数图象大致是( )

-
14.
(2024·海港模拟)
《九章算术》是中国传统数学的重要著作,书中有一道题“今有五雀六燕,集称之衡,雀俱重,燕俱轻;一雀一燕交而处,衡适平;并燕雀重一斤问:燕雀一枚,各重几何?”译文:“五只雀、六只燕,共重1斤(古时1斤=16两).雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕重量各为多少?”设雀重x两,燕重y两,可列出方程组( )
-
15.
(2024·海港模拟)
抛物线

与

轴交于点
A、
B A
A在

左侧

两点与抛物线的顶点构成的三角形,当内心与外心正合时,此时抛物线顶点记为点

.若拋物线的顶点到
x轴的距离比点
C到
x轴的距离大时,求
a的取值范围.甲求得

;乙求得

.下列说法正确的是( )
A . 甲对乙错
B . 甲错乙对
C . 二人答案合在一起才正确
D . 二人答案合在一起也不正确
-
16.
(2024·海港模拟)
如图,在

中,点
E、
F分别在边
AD、
BC上,点
G、
H在对角线
BD上,且

, 关于四边形
EGFH , 下列说法正确的个数是( )

①四边形EGFH一定是平行四边形且有无数个;
②四边形EGFH可以是矩形且有无数个;
③四边形EGFH可以是菱形且有无数个;
④四边形EGFH可以是正方形且有无数个;
A . 1个
B . 2个
C . 3个
D . 4个
二、填空题(本大题共3个小题,共10分.17小题2分,18~19小题各4分,每空2分
-
-
18.
(2024·海港模拟)
我们知道平行四边形具有不稳定性,即:当平行四边形的四条边确定时,得到的平行四边形是不唯一的.如图,

中,

.
① 的面积的最大值为.
的面积的最大值为.
②当 面积变为最大面积的一半时,则
面积变为最大面积的一半时,则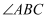 等于°.
等于°.
-
19.
(2024·海港模拟)
如图,正六边形
ABCDEF的边长为2,内部有一个正方形(正方形的顶点可以在正六边形的边上),正方形的两个顶点
M、
N分别在边
AF、
CD上.

①如图1, 则正方形的边长为.
则正方形的边长为.
②正方形面积的最大值为.
三、解答题(本大题共7个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
20.
(2024·海港模拟)
定义新运算:对于任意实数
a ,
b(
a≠0),都有

, 等式右边是通常的加、减、除运算,例如:

.
-
(1)
求

的值.
-
(2)
若

, 求

的值.
-
-
(1)
当

时,请你化简:

;
-
(2)
嘉琪说:“当

时,无论

取何值时,

总是非正数;”嘉琪的说法是否正确?并论证你的判断.
-
22.
(2024·海港模拟)
某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上(含6分)为合格,达到9分以上(含9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条型统计图如下:

-
(1)
完成下表:
组别 | 平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲 | 6.7 | | 6 | 3.41 | | 20% |
乙 | | 7.5 | | 1.69 | 80% | 10% |
-
(2)
甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为乙组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
-
(3)
从甲、乙两组优秀的学生中抽取两名同学参加比赛,求两名都是甲组学生的概率.
-
23.
(2024·海港模拟)
如图,

中,

为
BC中点,以

为圆心,
BD长为半径作

, 交
AB与点
E.
M为

上一点,连接
AM , 将
AM绕
A点顺时针旋转∠
BAC的度数,得线段
AN、连接
CM、
BN.

-
(1)
求证:

-
(2)
当点
M与点

重合时,求证:
AN与

相切;
-
(3)

面积的最大值为
.
-
24.
(2024·海港模拟)
如图是8个台阶的示意图(各拐角均为90°),每个台阶宽、高分别为2和1.
A1B1为第一个台阶面,
A2B2为第二个台阶面,以此类推,..,
A8M为第八个台阶面.

-
(1)
求直线MN的解析式;并判断B1是否在直线MN上;
-
(2)
点

(填“在”或“不在”)直线
MN上;点

在直线
上;
-
(3)
嘉琪同学拿着激光笔照射台阶,射出的光线可以看成直线:

若使光线照到所有台阶,求
m的取值范围;
-
(4)
蚂蚁(看做点
P)从
N出发,沿

爬到点
M , 爬行的平均速度为每秒2个单位长度,爬行时间为
t秒.当点
P(
a ,
b)在第
n个台阶面上时,直接用含
n、
t的式子表示点
P的横坐标,并用含
n的式子写出
t的取值范围.
-
25.
(2024·海港模拟)
如图是某数学:学习小组设计的动画游戏,

轴上依次何一个正方形
ABCD、矩形
EFGH、正方形
LMNR , 其中

分别为
BC、
AD的中点,以直线
OS为

轴建立平面直角坐标系.从点

处向右上方沿拋物线

:

发出一个带光的点

.点

落在矩形
EFGH的边
EH上后立即弹起,形成最大高度为7的抛物线

;落在正方形
LMNR的边
LR上后又立即弹起形成最大高度为3的抛物线

, 经过两次弹起后点

落在

轴上,已知

形状相同.

-
-
(2)
求点

第一次弹起后形成的拋物线

的解析式;
-
(3)
左右平移发出点

的位置(点

只能在
AD边上发出,其他保持不变)若使点
P只经过一次弹起后就能落在

轴上,直接写出点

的移动方向和移动距离

的取值范围.
-
-
-
(2)
求证:

.
-
(3)
如图2,将与

全等的

如图放置,
EF与
BC重合,

点与

点重合,将

沿
BC方向向右平移,平移速度为每秒1个单位长度,如图3.当点
E到达点

后立即绕点

逆时针旋转,旋转的速度为每秒

, 如图4,当

点落在直线
BC上时停止旋转.
①从平移开始到旋转结束,求点D经过路径的长度.
②求点M落在 内部(包含边界)的时长.
内部(包含边界)的时长.
③在旋转过程中,设DE、EF与 的边分别交于点P、Q , 当
的边分别交于点P、Q , 当 时,直接写出
时,直接写出 的值.(参考数据:
的值.(参考数据: )
)
(第一步)
(第二步)
(第三步)
的高AD和角平分线AE , 若
点在线段BD上,则说明
.
 B .
B .  C .
C .  D .
D . 


则正方形的边长为.



内部(包含边界)的时长.
的边分别交于点P、Q , 当
时,直接写出
的值.(参考数据:
)