一、单项选择题(本大题共6小题,每小题3分,共18分)
-
-
2.
(2024·大余模拟)
《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( ).
-
-
-
5.
(2024·大余模拟)
物理中有一种现象,叫折射现象,它指的是当光线从空气射入水中时,光线的传播方向会发生改变.如图,我们建立折射现象数学模型,

表示水面,它与底面

平行,光线

从空气射入水里时发生了折射,变成光线

射到水底

处,射线

是光线

的延长线.若

, 则

的度数为( )

-
二、填空题(本大题共6小题,每小题3分,共18分)
-
-
-
9.
(2024·大余模拟)
党的二十大报告中指出,我国已建成世界上规模最大的社会保障体系,基本养老保险覆盖1040000000人,请将数据1040000000用科学记数法表示为
.
-
10.
(2024·大余模拟)
某工厂接到加工600件衣服的订单,预计每天做25件,正好按时完成,后因客户要求提前3天交货,工人则需要提高每天的工作效率,设工人每天应多做

件,依题意列方程正确的是
.
-
11.
(2024·大余模拟)
如图,某校宣传栏BC后面12米处种有一排与宣传栏平行的若干棵树,即

, 且相邻两棵树的间隔为2米,一人站在距宣传栏前面的A处正好看到两端的树干,其余的树均被宣传栏挡住.已知

,

米,

米,该宣传栏后

处共有
棵树.(不计宣传栏的厚度).

-
12.
(2024·大余二模)
已知菱形

的边长为4,

, 点

在边

上且

,

是菱形

边上的一点,若

是以

为腰的等腰三角形,则

的面积为
.
三、解答题(本大题共5小题,每小题6分,共30分)
-
-
(1)
计算:

;
-
(2)
解不等式组:

.
-
14.
(2024·大余模拟)
图1与图2均为

的正方形网格,每个小正方形的顶点称为格点,点

均落在格点上,在图1、图2给定的网格中按要求作图.

-
(1)
在图1的格点中取一点

, 使

为等腰直角三角形;
-
(2)
在图2的格点中取一点

, 使

是与

面积相等的等腰三角形.
-
15.
(2024·大余模拟)
下面是学习了分式混合运算后,甲,乙两名同学解答一道题目中第一步的做法,选择其中一名同学的做法,完成解答过程.
我选择: ▲ 同学.
-
16.
(2024·大余模拟)
亮亮和爸爸搭乘飞机外出游玩.若航班售票系统随机分配座位,且系统已将两人分配到同一排.如下图所示的是飞机内同一排座位

,

,

,

的排列示意图.
-
(1)
亮亮被分配到座位


事件(填“必然”“不可能”或“随机”);
-
(2)
求亮亮和爸爸被分配到相邻座位的概率(过道两侧座位不算相邻).
-
17.
(2024·大余模拟)
如图,一次函数

与反比例函数

,

图象分别交于

,

,与

轴交于点

,连接

,

.
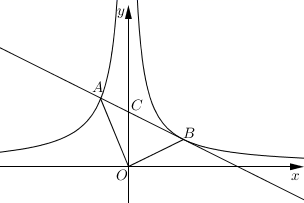
-
(1)
求反比例函数

和一次函数

的表达式;
-
(2)
求

的面积.
四、解答题(本大题共3小题,每小题8分,共24分)
-
18.
(2024·大余模拟)
全球工业互联网大会永久会址落户沈阳.为了让学生了解工业互联网相关知识,某校准备开展“工业互联网”主题日活动,聘请专家为学生做五个领域的专题报告:
A.数字孪生;B.人工智能;C.应用 ;D.工业机器人;E.区块链.为了解学生的研学意向,在随机抽取的部分学生中下发如图所示的调查问卷,所有问卷全部收回且有效,根据调查数据绘制成两幅不完整的统计图.
;D.工业机器人;E.区块链.为了解学生的研学意向,在随机抽取的部分学生中下发如图所示的调查问卷,所有问卷全部收回且有效,根据调查数据绘制成两幅不完整的统计图.
“工业互联网”主题日学生研学意向调查问卷 请在下列选项中选择您的研学意向,并在其后“☐”内打“√”(每名同学必选且只能选择其中一项),非常感谢您的合作. A.数字孪生☐ B.人工智能口 C.应用 ☐ D.工业机器人☐ E.区块链☐ ☐ D.工业机器人☐ E.区块链☐ |
“工业互联网”主题日学生研学意向调查结果统计图

请根据统计图提供的信总,解答下列问题:
-
(1)
求本次调查所抽取

学生人数,并直接补全条形统计图;
-
(2)
求扇形统计图中领域“

”对应扇形的圆心角的度数;
-
(3)
学校有

名学生参加本次活动,地点安排在两个多功能厅,每场报告时间为90分钟.由下面的活动日程表可知,

和

两场报告时间与场地已经确定.在确保听取报告的每名同学都有座位的情况下,请你合理安排

,

,

三场报告,补全此次活动日程表(写出一种方案即可),并说明理由.
“工业互联网”主题日活动日程表 |
地点(座位数) 时间 | 1号多功能厅 (200座) | 2号多功能厅 (100座) |

|
| 
|

| 
|
|

|
| 设备检修 暂停使用 |
-
19.
(2024·大余模拟)
中国传统建筑屋顶设计是中国古代建筑之瑰宝.常见的屋顶种类主要有院殿顶、歇山顶、硬山顶、悬山顶、攒尖顶、卷棚顶和平顶等.如图1的古代建筑屋顶,被称为“悬山顶”,它的侧视图呈轴对称图形,如图2所示,已知屋檐

米,屋顶E到支点C的距离

米,墙体高

米,屋面坡角

. (参考数值:

)

-
(1)
求房屋内部宽度

的长;
-
(2)
求点A与屋面

的距离.
-
20.
(2024·大余模拟)
2023年我国多地阴雨连绵,夏粮作为全年粮食生产的第一季,收割受到极大的影响.陕西省某县政府为了帮助村民抢收小麦,租来了每天能收割4公顷小麦的

型收割机和每天能收割6公顷小麦的

型收割机共

台,全部型号的收割机一天能收割

公顷.
-
-
(2)
该县某乡镇共有

公顷小麦,镇长向县政府申请了援助.因调配问题,县政府只能每天向该镇派遣同一型号的所有收割机进行援助.经过3天的努力,该乡镇恰好收割了全部小麦.已知每台

型收割机收费是

元/天,每台

型收割机收费是

元/天,则援助该乡镇共花费了多少元?
五、解答题(本大题共2小题,每小题9分,共18分)
-
-
(1)
课本再现:如图1,

是

的两条切线,切点分别为A,B.则图中的

与

,

与

有什么关系?请说明理由,
-
(2)
知识应用:如图,

分别与

相切于点A、B、C,且

, 连接

, 延长

交

于点M,交

于点E,过点M作

交

于N.
①求证: 是
是 的切线:
的切线:
②当 cm,
cm, cm时,求
cm时,求 的半径及图中阴影部分的面积.
的半径及图中阴影部分的面积.
-
-
(1)
试判断四边形

的形状,并说明理由;
-
(2)
如图②,若

, 请猜想线段

与

的数量关系并加以证明;
-
(3)
解决问题:
如图①,若 ,
,  , 请直接写出
, 请直接写出 的长.
的长.
六、解答题(本大题共12分)
-
23.
某数学兴趣小组运用《几何画板》软件探究

型抛物线图象.发现:如图1所示,该类型图象上任意一点P到定点

的距离

, 始终等于它到定直线l:

的距离

(该结论不需要证明).他们称:定点F为图象的焦点,定直线l为图象的准线,

叫做抛物线的准线方程.准线l与y轴的交点为H.其中原点O为

的中点,

. 例如,抛物线

, 其焦点坐标为

, 准线方程为l:

, 其中

,

.

-
(1)
【基础训练】
请分别直接写出抛物线 的焦点坐标和准线l的方程:,;
的焦点坐标和准线l的方程:,;
-
(2)
【技能训练】
如图2,已知抛物线 上一点
上一点 到焦点F的距离是它到x轴距离的3倍,求点P的坐标;
到焦点F的距离是它到x轴距离的3倍,求点P的坐标;
-
-
 B .
B .  C .
C .  D .
D . 
![]()


;D.工业机器人;E.区块链.为了解学生的研学意向,在随机抽取的部分学生中下发如图所示的调查问卷,所有问卷全部收回且有效,根据调查数据绘制成两幅不完整的统计图.



是
的切线:
cm,
cm时,求
的半径及图中阴影部分的面积.
,
, 请直接写出
的长.

的焦点坐标和准线l的方程:,;
上一点
到焦点F的距离是它到x轴距离的3倍,求点P的坐标;
的焦点为F,准线方程为l.直线m:
交y轴于点C,抛物线上动点P到x轴的距离为
, 到直线m的距离为
, 请直接写出
的最小值;
平移至
. 抛物线
内有一定点
, 直线l过点
且与x轴平行.当动点P在该抛物线上运动时,点P到直线l的距离
始终等于点P到点F的距离(该结论不需要证明).例如:抛物线
上的动点P到点
的距离等于点P到直线l:
的距离.
是第二象限内一定点,点P是抛物线
上一动点,当
取最小值时,请求出
的面积.