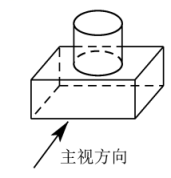
 B .
B . 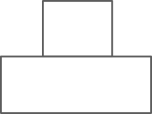 C .
C . 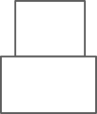 D .
D . 


图1 图2



①若 , 设点
的横坐标为
, 点
的横坐标为
, 则
与
关系为;
②在①的条件下,若的面积是4.5,则
的值为.

图①空白部分小正方形的个数是
图②空白部分小正方形的个数是
图③空白部分小正方形的个数是+.
.

类别 | A类 | B类 | C类 | D类 |
阅读时长 | ||||
频数 | 8 | 4 |

请根据图表中提供的信息解答下面的问题:

图1

图2

图3
①确定的形状,并说明理由;
②若 ,
, 求等联线
和线段
的长.

①探究直线在运动过程中,线段
是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
②当点为抛物线顶点时,求
的面积.