江西省抚州市黎川县黎川一中片区八校联考2023-2024学年...

更新时间：2024-06-14 浏览次数：3 类型：期中考试

一、单选题（本大题共6小题，每小题3分，共18分）

1. (2024七上·会泽期中) －2024的倒数是（）

A . －2024 B . 2024 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024九下·黎川期中) 如图是由6个相同的小正方体搭成的几何体，若去掉上层的一个小正方体，则下列说法正确的是（）．

A . 主视图一定变化 B . 左视图一定变化 C . 俯视图一定变化 D . 三种视图都不变化

答案解析收藏纠错 + 选题
3. (2024九下·黎川期中) 春节期间，贴春联，送祝福一直是我们的优良传统．我国传统文化中的“福禄寿喜”图（如图）由四个图案构成．这四个图案中是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024九下·黎川期中) 下列运算中，结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九下·黎川期中) 烷烃是一类由碳、氢元素组成的有机化合物，在生产生活中可作为燃料、润滑剂等原料，也可用于动、植物的养护．通常用碳原子的个数命名为甲烷、乙烷、丙烷、 $\text{[math]}$ 、癸烷（当碳原子数目超过10个时即用汉文数字表示，如十一烷、十二烷 $\text{[math]}$ 等，甲烷的化学式为 $\text{[math]}$ ，乙烷的化学式为 $\text{[math]}$ ，丙烷的化学式为 $\text{[math]}$ ，其分子结构模型如图所示，按照此规律，十二烷的化学式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九下·黎川期中) 如图，抛物线 $\text{[math]}$ 的对称轴为直线 $\text{[math]}$ ，且过点 $\text{[math]}$ ．现有以下结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③对于任意实数 $\text{[math]}$ ，都有 $\text{[math]}$ ；④若点 $\text{[math]}$ 是图象上任意两点，且 $\text{[math]}$ ，则 $\text{[math]}$ ，其中正确的结论是（）

A . ①② B . ②③④ C . ①②④ D . ①②③④

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题3分，共18分）

7. (2024九上·东台模拟) 分解因式： $\text{[math]}$ =．

答案解析收藏纠错 + 选题
8. (2024九下·黎川期中) 某细菌的直径0.00000054米，0.00000054米用科学记数法表示为米．

答案解析收藏纠错 + 选题
9. (2024九下·长沙模拟) 若 $\text{[math]}$ ， $\text{[math]}$ 是方程 $\text{[math]}$ 的两个根，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
10. (2024九下·黎川期中) 如图，电路上有3个开关 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 和1个小灯泡L，任意闭合电路上2个开关，小灯泡发光的概率为．

答案解析收藏纠错 + 选题
11. (2024九下·黎川期中) 把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为．

答案解析收藏纠错 + 选题
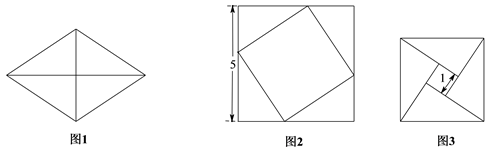
12. (2024九下·黎川期中) 在平面直角坐标系中，已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点D在直线BC上， $\text{[math]}$ ，点P是y轴上一动点，若 $\text{[math]}$ ，则点P的坐标是．

答案解析收藏纠错 + 选题

三、解答题（本大题共5小题，每小题6分，共30分）

13. (2024九下·黎川期中)
1. （1）计算： $\text{[math]}$ ．
2. （2）如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， D、E、F分别是AB、AC、BC的中点连接DE、DF ，求证：四边形DFCE是菱形．
答案解析收藏纠错 + 选题
14. (2024九下·黎川期中) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2024九下·黎川期中) 如图，点A ， B ， C在 $\text{[math]}$ 上，且 $\text{[math]}$ ，请仅用无刻度的直尺，按照下列要求作图．（保留作图痕迹，不写作法）
1. （1）在图（1）中， $\text{[math]}$ ，作一个度数为30°的圆周角；
2. （2）在图（2）中， $\text{[math]}$ ，作一个顶点均在 $\text{[math]}$ 上的等边三角形．
答案解析收藏纠错 + 选题
16. (2024九下·黎川期中) 一个不透明的口袋中装有四个完全相同的小球，上面分别标有数字1，2，3，4．
1. （1）从口袋中随机摸出一个小球，求摸出小球上的数字是奇数的概率（直接写出结果）；
2. （2）先从口袋中随机摸出一个小球，将小球上的数字记为x，在剩下的三个小球中再随机摸出一个小球，将小球上的数字记为y．请用列表或画树状图法，求由x，y确定的点 $\text{[math]}$ 在函数 $\text{[math]}$ 的图象上的概率．
答案解析收藏纠错 + 选题
17. (2024九下·黎川期中) 如图，一次函数y=kx+b的图象与反比例函数y=− $\text{[math]}$ 的图象相交于A(−1，m)和B(n，−1)两点．
1. （1） m=，n=；
2. （2）求出一次函数的解析式，并结合图象直接写出不等式kx+b>− $\text{[math]}$ 的解集．
答案解析收藏纠错 + 选题

四、解答题（本大题共3小题，每小题8分，共24分）

18. (2024九下·黎川期中) 中国自古就是礼仪之邦，平辈行礼，上半身前弯15°，晚辈行礼，上半身前弯45°．小贤同学路遇李老师，面向李老师行了一个45°的作揖礼，李老师面向小贤回了一个15°的作揖礼（如图1）．现将其简化成如图2所示，已知李老师身高 $\text{[math]}$ ，上半身身高 $\text{[math]}$ ，小贤身高 $\text{[math]}$ ，上半身身高 $\text{[math]}$ ．
1. （1）求当李老师回礼时，其头部距地面的高度．
2. （2）行礼之时，人与人之间应该保持100cm以上的距离（指头与头之间的水平距离）最为适宜．行礼前，小贤距李老师180cm，请问同时行礼、回礼时，李老师与小贤之间的距离是否适宜？（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
19. (2024九下·黎川期中) 天气越来越热，市民出行纷纷撑伞防晒，某商场抓住这一商机，先用3200元购进一批防紫外线太阳伞，很快就销售一空，商场又用8000元购进了第二批这种太阳伞，所购数量是第一批的2倍，但每把太阳伞贵了4元，商场在销售这种太阳伞时，每把定价都是50元，每天可卖出20把．
1. （1）求两次共购进这种太阳伞多少把；
2. （2）商场为了加快资金的回笼速度，打算对第二批太阳伞进行降价销售，经市场调查，如果这种太阳伞每把降价1元，则每天可多售出2把，则太阳伞每把降价多少元时，才能使商场每天的销售额最大？并求出销售额的最大值．
答案解析收藏纠错 + 选题
20. (2024九下·黎川期中) 某学校要调查学生关于“新冠肺炎”防治知识的了解情况，从七、八年级各随机抽取了10名学生进行测试（百分制），测试成绩整理、描述和分析如下：
七、八年级抽取的学生成绩统计表
年级
七年级
八年级
平均数
92
92
中位数
93
b
众数
c
100
方差
52
50.4
（成绩得分用x表示，共分成四组：A ． $\text{[math]}$ ， B ． $\text{[math]}$ ， C ． $\text{[math]}$ ， D ． $\text{[math]}$ ），七年级10名学生的成绩是：96，80，96，86，99，96，90，100，89，82．八年级10名学生的成绩在C组中的数据是：94，90，92．
根据以上信息，解答下列问题：
1. （1）直接写出上述图表中a ， b ， c的值；
2. （2）根据以上数据，你认为该校七、八年级中哪个年级学生掌握“新冠肺炎”知识较好？请说明理由．
3. （3）该校七、八年级共1200人参加了此次调查活动，估计参加此次调查活动成绩优秀（ $\text{[math]}$ ）的学生人数是多少？
答案解析收藏纠错 + 选题

五、解答题（本大题共2小题，每小题9分，共18分）

21. (2024九下·黎川期中) 课本再现
1. （1）在圆周角和圆心角的学习中，我们知道了：圆内接四边形的对角互补．课本中先从四边形一条对角线为直径的特殊情况来论证其正确性，再从对角线是非直径的一般情形进一步论证其正确性，这种数学思维方法称为“由特殊到一般”．
  如图1，四边形ABCD为 $\text{[math]}$ 的内接四边形，AC为直径，则 $\text{[math]}$ 度， $\text{[math]}$ 度．
2. （2）如果 $\text{[math]}$ 的内接四边形ABCD的对角线AC不是 $\text{[math]}$ 的直径，如图2、图3，请选择一个图形证明：圆内接四边形的对角互补．
3. （3）知识运用
  如图4，等腰三角形ABC的腰AB是 $\text{[math]}$ 的直径，底边和另一条腰分别与 $\text{[math]}$ 交于点D ， E ．点F是线段CE的中点，连接DF ，求证：DF是 $\text{[math]}$ 的切线．
答案解析收藏纠错 + 选题
22. (2024九下·黎川期中) 已知抛物线 $\text{[math]}$ ： $\text{[math]}$ ．
1. （1）下列有关抛物线 $\text{[math]}$ 的结论正确的有（填序号）．
  ①开口向下；
  ②对称轴在y轴的左侧；
  ③与y轴的交点坐标为 $\text{[math]}$ ；
  ④函数值y有最小值 $\text{[math]}$ ；
2. （2）当 $\text{[math]}$ 时，抛物线 $\text{[math]}$ 的顶点坐标为，将抛物线 $\text{[math]}$ 沿直线 $\text{[math]}$ 翻折得到抛物线 $\text{[math]}$ ，则抛物线 $\text{[math]}$ 的表达式为；
3. （3）如图，设抛物线 $\text{[math]}$ 与y轴相交于点C ，将抛物线 $\text{[math]}$ 沿直线 $\text{[math]}$ 翻折，得到抛物线 $\text{[math]}$ ，抛物线 $\text{[math]}$ ， $\text{[math]}$ 的交点为A ，抛物线 $\text{[math]}$ 的顶点为P ．是否存在实数m ，使得 $\text{[math]}$ ？若存在，请求出m的值；若不存在，请说明理由．
答案解析收藏纠错 + 选题

六、解答题（本大题共12分）

23. (2024九下·黎川期中)
1. （1）【问题发现】如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D为BC的中点，以BD为一边作正方形BDFE ，点F恰好与点A重合，则线段CF与AE的数量关系为；
2. （2）【拓展探究】在（1）的条件下，如果正方形BDFE绕点B顺时针旋转，连接CF ， AE ， BF ，线段CF与AE的数量关系有无变化？请仅就图2的情形给出证明；
3. （3）【问题解决】当 $\text{[math]}$ ，且（2）中的正方形BDFE绕点B顺时针旋转到E ， F ， C三点共线时，求出线段AE的长．
答案解析收藏纠错 + 选题