广西壮族自治区南宁市青秀区第十四中学2023-2024学年八...

更新时间：2024-08-27 浏览次数：3 类型：期中考试

一、选择题（共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑．）

1. (2024八下·青秀期中) 下列二次根式中是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·青秀期中) 一个直角三角形的两条直角边分别是 $\text{[math]}$ 和 $\text{[math]}$ ，斜边长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024八下·青秀期中) 如图，已知四边形 $\text{[math]}$ 是平行四边形， $\text{[math]}$ 是它的两条对角线，下列条件中能判定这个平行四边形为矩形的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024八下·青秀期中) 若一次函数 $\text{[math]}$ 的函数值 $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024八下·青秀期中) 在学校开展的劳动实践活动中，生物兴趣小组7个同学采摘到西红柿的质量（单位： kg ）分别是：5，9，5，6，4，5，7，则这组数据的众数和中位数分别是（）

A . 6，6 B . 4，6 C . 5，6 D . 5，5

答案解析收藏纠错 + 选题
6. (2024八下·青秀期中) 如图，直线 $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，则关于 $\text{[math]}$ 的二元一次方程组 $\text{[math]}$ 的解为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024八下·青秀期中) 顺次连接任意一个四边形各边中点所得到的四边形一定是（）

A . 矩形 B . 菱形 C . 平行四边形 D . 正方形

答案解析收藏纠错 + 选题
8. (2024八下·青秀期中) 若一次函数 $\text{[math]}$ 的图象向下平移3个单位后经过点 $\text{[math]}$ ，则b的值为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
9. (2024八下·青秀期中) 如图，在矩形COED中，点D的坐标是(1，3)，则CE的长是（）

A . 3 B . $\text{[math]}$ C . $\text{[math]}$ D . 4

答案解析收藏纠错 + 选题
10. (2024八下·青秀期中) “五一节”期间，数学老师一家自驾游去了离家170千米的某地，下面是他们离家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象．他们出发2.2小时时，离目的地还有（）千米．

A . 12 B . 24 C . 146 D . 164

答案解析收藏纠错 + 选题
11. (2024八下·青秀期中) 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，则线段 $\text{[math]}$ 的长为（）

A . 4 B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024八下·青秀期中) 将矩形纸板剪掉一个小矩形后剩余部分如图1所示，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发，沿路径 $\text{[math]}$ 匀速运动，速度为 $\text{[math]}$ ，点 $\text{[math]}$ 到达终点 $\text{[math]}$ 后停止运动， $\text{[math]}$ 的面积 $\text{[math]}$ 与点 $\text{[math]}$ 运动的时间（s）的关系如图2所示，根据图象获取了以下的信息：① $\text{[math]}$ ；② $\text{[math]}$ ；③点 $\text{[math]}$ 从点 $\text{[math]}$ 运动到点 $\text{[math]}$ 需要 $\text{[math]}$ s；④矩形纸板裁剪前后周长均为 $\text{[math]}$ ．其中正确信息的个数有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题

二、填空题（本大题共6小题，每小题2分，共12分．）

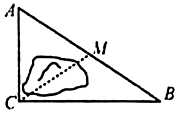
13. (2024八下·青秀期中) 直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交点坐标为.

答案解析收藏纠错 + 选题
14. (2024八下·青秀期中) 如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开．若测得AB的长为10km，则M，C之间的距离是km．

答案解析收藏纠错 + 选题
15. (2024八下·从化期末) 甲、乙、丙、丁四名同学参加立定跳远训练，他们成绩的平均数相同，方差如下： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则成绩最稳定的同学是．（填写甲或乙、丙、丁）

答案解析收藏纠错 + 选题
16. (2024八下·青秀期中) 阅读材料：在进行二次根式运算中，经常会出现诸如 $\text{[math]}$ 的计算，需要运用分式的基本性质，将分母转化成有理数，这就是分母有理化．例如： $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ，根据材料化简： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2024八下·青秀期中) 如图，点P（﹣4，3）在一次函数y＝kx＋b（k≠0）的图象上，则关于x的不等式kx＋b＜3的解集是.

答案解析收藏纠错 + 选题
18. (2024八下·青秀期中) 如图， $\text{[math]}$ 中，分别以这个三角形的三边为边长作正方形，面积分别记为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ．如果 $\text{[math]}$ ，则阴影部分的面积为．

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，共72分．解答应写出文字说明、证明过程或演算步骤．）

19. (2024八下·青秀期中) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2024八下·青秀期中) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2024八下·青秀期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 交于点 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 上， $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是平行四边形；
2. （2）若 $\text{[math]}$ 求证：四边形 $\text{[math]}$ 是菱形．
答案解析收藏纠错 + 选题
22. (2024八下·青秀期中) 联合国教科文组织将每年的3月14日定为“国际数学日”．某校八年级在三月份开展了以“数学文化”为主题的阅读活动，并随机抽查了部分学生在活动期间阅读相关文章的篇数．
收集数据：15，12，15，13，15，15，12，18，15，18，18，15，13，15，12，15，13，15，18，18；
整理数据：
阅读文章（篇）
12
13
15
18
人数（人）
3
$\text{[math]}$
9
5
请你根据提供的信息解答下列问题：
1. （1）直接写出 $\text{[math]}$ 的值及学生阅读篇数的中位数；
2. （2）求本次调查学生阅读篇数的平均数；
3. （3）若该年级有300名学生，请你估计该校八年级学生阅读关于“数学文化”的文章共多少篇？
答案解析收藏纠错 + 选题
23. (2024八下·青秀期中) 阅读下列一段文字，回答问题．
【材料阅读】平面内两点 $\text{[math]}$ ， $\text{[math]}$ ，则由勾股定理可得，这两点间的距离 $\text{[math]}$ ．
例如，如图1， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．
【直接应用】
1. （1）已知 $\text{[math]}$ ，求 $\text{[math]}$ 两点间的距离；
2. （2）如图2，在平面直角坐标系中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与x轴正半轴的夹角是45度．
  ①求点 $\text{[math]}$ 的坐标；
  ②试判断 $\text{[math]}$ 的形状．
答案解析收藏纠错 + 选题
24. (2024八下·青秀期中) 某商场购进 $\text{[math]}$ 两种商品共200件进行销售，其中 $\text{[math]}$ 商品的件数不大于 $\text{[math]}$ 商品的件数，且不少于50件， $\text{[math]}$ 两种商品的进价、售价如下表：

$\text{[math]}$
$\text{[math]}$
进价（元/件）
150
130
售价（元/件）
220
195
1. （1）设商场购进 $\text{[math]}$ 商品的件数为 $\text{[math]}$ 件，购进 $\text{[math]}$ 两种商品全部售出后获得利润为 $\text{[math]}$ 元，求 $\text{[math]}$ 和 $\text{[math]}$ 之间的函数关系式，并写出 $\text{[math]}$ 的取值范围；
2. （2）在（1）的条件下，要使商场获得最大利润，该公司应购进 $\text{[math]}$ 多少件？最大利润是多少？
3. （3）在（1）的条件下，商场决定在销售活动中每售出一件 $\text{[math]}$ ，就从一件 $\text{[math]}$ 的利润中拿出 $\text{[math]}$ 元 $\text{[math]}$ 捐给慈善基金，求该商场售完所有商品并捐献慈善资金后获得的最大利润．
答案解析收藏纠错 + 选题
25. (2024八下·青秀期中) 如图，已知正方形 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，射线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ．
2. （2）判断 $\text{[math]}$ 的形状，并说明理由．
3. （3）作 $\text{[math]}$ 的中点 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
26. (2024八下·青秀期中) 在平面直角坐标系中，线段 $\text{[math]}$ 的端点分别为 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 所在直线的表达式．
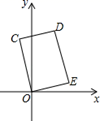
2. （2）如图，点 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 从点 $\text{[math]}$ 沿 $\text{[math]}$ 以每秒2个单位长度的速度运动到点 $\text{[math]}$ ，设运动时间为秒．
  ①连接 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 的周长最短时，求点 $\text{[math]}$ 的坐标；
  ②当直线 $\text{[math]}$ 与线段 $\text{[math]}$ 有交点时，直接写出的取值范围．
答案解析收藏纠错 + 选题