一、选择题(本题共10个小题,每小题4分,满分共32分,每小题四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
-
-
-
-
-
A .  B . 1
C . 2
D .
B . 1
C . 2
D . 
-
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
-
7.
(2024八上·成都期中)
如图,分别以直角三角形的三边为直径向三角形外作三个半圆,图中的字母是它们的面积其中

,

, 则

为( )

A . 8π
B . 4π
C . 16π
D . 4
-
A . ①②④
B . ①③⑤
C . ②③④
D . ①④⑤
二、填空题(本题共5个小题,每小题4分,满分共20分,答案写在答题卡上)
-
-
-
-
12.
(2024八上·成都期中)
如图,在数轴上,点A所对应的实数为-1,点C对应的实数为2,过C作数轴的垂线段BC,使得BC = 1,再以A为圆心,AB长为半径画弧,交数轴的正半轴于点D,则点D对应的实数为

-
13.
(2024八上·成都期中)
如图,在

中,按以下步骤作图:①分别以点B和C为圆心,以大于

的长为半径作弧,两弧相交于点M和N;②作直线

交

于点D,连接

, 若

. 则

的周长为
.

三、解答题(本大题共5个小题,满分共48分,答案写在答题卡上)
-
-
(1)

-
(2)

-
-
(1)
已知

. 求

的值.
-
(2)
若

, 求

的平方根.
-
-
(1)
画出

关于x轴对称的图形

, 并写出顶点

的坐标;
-
(2)
求

的面积.
-
(3)
求点B到

的距离.
-
17.
(2024八上·成都期中)
如图所示,在一次消防演习中,消防员架起一架25米长的云梯,斜靠在一面墙上,梯子底端C离墙24米.

-
-
(2)
如果消防员接到命令,要求梯子的顶端上升8米(云梯长度不变),那么云梯底端在水平方向应滑动多少米?
-
四、填空题(本大题共5个小题,每小题4分,满分共20分,答案写在答题卡上)
-
-
-
21.
(2024八上·成都期中)
在平面直角坐标系中,点

经过某种变换后得到点

, 我们把点

叫做点

的终结点.已知点

的终结点为

, 点

的终结点为

, 点

的终结点为

, 这样依次得到

、

、

、

、…、

、…,若点

的坐标为

, 则点

的坐标为
.
-
22.
(2024八上·成都期中)
如图,长方形

中,

,

, 点E为射线

上一动点(不与D重合),将

沿AE折叠得到

, 连接

, 若

为直角三角形,则


-
五、解答题(本大题共3个小题,满分共30分,答案写在答题卡上)
-
-
(1)
观察上面的解答过程,请写出

_____;
-
(2)
利用上面的解法,请化简:

-
(3)

和

的值哪个较大,请说明理由.
-
-
-
(2)
已知点

, 在y轴上是否存在点P,使

是等腰三角形?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由;
-
(3)
若x轴上有一动点D,将

绕点D逆时针旋转

为

, 在点D运动过程中,连接

, 则

是否有最小值?若有,则

的最小值=_____,此时Q的坐标为_____,D的坐标为____;若没有,请说明理由.
-
-
(1)
如图1,判断

与

的关系并证明;
-
(2)
如图2,连接

, 当

时,试探究线段

和

的数量关系并说明理由;
-
(3)
如图3,O是斜边

的中点,M为

上方一点,且
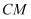
与斜边

的交点在线段

上,若

, 求

的长.
和
是同类二次根式;②
的平方根是3;③
位于第三象限;④
的算术平方根是
;⑤若
, 则点
在第二、四象限角平分线所在直线上.



中,
, 以
为边在
外部作等边
, 连接
, 求
的面积.

中,
, 若
面积为21且
的长为8,求
的面积.
