一、单选题(本大题共10小题,每小题3分,共30分;在每小题给出的四个选项中,只有一项是符合题目要求的)
-
-
-
-
4.
(2024九上·广州期中)
如图,有一个底部呈球形的烧瓶,球的半径为

, 瓶内液体已经过半,最大深度

, 则截面圆中弦

的长为( )

-
5.
(2024九上·广州期中)
如图,把小圆形场地的半径增加

得到大圆形场地,场地面积扩大了一倍.若设小圆形场地的半径为

, 那么列方程正确的是( )

-
6.
(2024九上·广州期中)
如图,在

中,

, 将

绕点A按逆时针方向旋转得到

. 若点

恰好落在BC边上,且

, 则
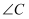
的度数为( )

-
-
8.
(2024九上·广州期中)
如图所示的暗礁区,两灯塔A,B之间的距离恰好等于圆半径的

倍,为了使航船S不进入暗礁区,那么S对两灯塔A,B的视角

必须( )

A . 大于 B . 小于
B . 小于 C . 大于
C . 大于 D . 小于
D . 小于
-
-
10.
(2024九上·广州期中)
如图,

点是圆

劣弧

上的一个动点(不与点

,

重合),且满足

,

是

内一点,

,

,

, 点

在劣弧

上运动的过程中,

, 则

的值满足( )

二、填空题(本大题共6小题,每小题3分,共18分;)
-
-
-
-
-
15.
(2024九上·广州期中)
如图,

的直径

,

,

分别是它的两条切线,

与

相切于点

, 并与

,

分别交于

,

两点,

,

, 则

关于

的函数表达式为
.

-
16.
(2024九上·广州期中)
在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,若线段MA绕点M旋转得线段MA
' .
(1)如图①,线段MA'的长=.
(2)如图②,连接A'C,则A'C长度的最小值是.

三、解答题(本大题共9小题,满分72分.解答应写出文字说明、证明过程或演算步骤.)
-
-
-
(1)
以点

为旋转中心,把

逆时针旋转

, 画出旋转后的

;
-
(2)
在(1)的条件下,求线段

扫过的图形面积.
-
-
(1)
求证:无论

取任何实数,此方程总有两个不相等的实数根;
-
(2)
设

的两个实数根为

, 若

, 求出

的最小值.
-
-
(1)
求证:

;
-
-
21.
(2024九上·广州期中)
世界杯足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于12元.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每涨1元,每天销售量减少10本,现商店决定提价销售.销售单价为x元.
-
(1)
当每本足球纪念册销售单价是多少元时,商店每天获利2400元?
-
(2)
将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润w元最大?最大利润是多少元?
-
-
-
(2)
根据图象直接回答:当

取何值时,

;
-
(3)
连接

、

, 若点

在抛物线上,且

, 求点

的坐标.
-
-
(1)
尺规作图,补全图形:作

的垂直平分线交

于点E,交

于点F,连接

;
-
(2)
判断直线

与

的位置关系,并说明理由;
-
-
-
(1)
当抛物线也经过点

时,求m和n的值;
-
-
(3)
在(1)的条件下,抛物线与x轴的另一交点为B,与y轴交于点C,连接

, 点D是第一象限内抛物线上的一个动点,连接

, 与

, y轴分别交于点E,F,记三角形

,

的面积分别为

,

, 求

的最大值.
-
-
(1)
如图1,

、

是

的等垂弦,

,

垂足分别为D,E.
求证:四边形 是正方形;
是正方形;
-
(2)
如图2,

是

的弦,作

,

分别交

于D,C两点,连接

. 分别交

、

与点

、点

.
求证: ,
,  是
是 的等垂弦;
的等垂弦;
-
(3)
已知

的直径为10,

、

是

的等垂弦,P为等垂点.若

. 求

的长.
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 


是正方形;
,
是
的等垂弦;