1. (2019九上·惠山期末) （发现问题）爱好数学的小明在做作业时碰到这样的一道题目：

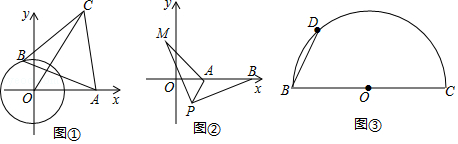
如图①，点O为坐标原点，⊙O的半径为1，点A（2，0）．动点B在⊙O上，连结AB，作等边△ABC（A，B，C为顺时针顺序），求OC的最大值

（解决问题）小明经过多次的尝试与探索，终于得到解题思路：在图①中，连接OB，以OB为边在OB的左侧作等边三角形BOE，连接AE．

1. （1） 请你找出图中与OC相等的线段，并说明理由；
3. （2） 求线段OC的最大值．

   （灵活运用）

5. （3） 如图②，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA＝2，PM＝PB，∠BPM＝90°，求线段AM长的最大值及此时点P的坐标．

   （迁移拓展）

7. （4） 如图③，BC＝4 ，点D是以BC为直径的半圆上不同于B、C的一个动点，以BD为边作等边△ABD，请直接写出AC的最值．