江苏省无锡市惠山区2019届九年级上学期数学期末考试试卷

更新时间：2019-06-12 浏览次数：412 类型：期末考试

一、单选题

1. (2019九上·惠山期末) 抛物线 $\text{[math]}$ 的顶点坐标是（）

A . （1，2） B . （1，-2） C . （-1，2） D . （-1，-2）

答案解析收藏纠错 + 选题
2. (2019九上·惠山期末) 一元二次方程x²=2x的根是（）

A . x=2 B . x=0 C . x₁=0， x₂=2 D . x₁=0, x₂=－2

答案解析收藏纠错 + 选题
3. (2021九上·高邮期末) 已知点A在半径为r的⊙O内，点A与点O的距离为6，则r的取值范围是（）

A . r ＜ 6 B . r ＞ 6 C . r ≥ 6 D . r ≤ 6

答案解析收藏纠错 + 选题
4. (2024九下·呼兰模拟) 在Rt△ABC中，∠C=90°，∠B=35°，AB=7，则BC的长为（）

A . 7sin35° B . $\text{[math]}$ C . 7cos35° D . 7tan35°

答案解析收藏纠错 + 选题
5. (2019九上·惠山期末) 在比例尺是1：8000的南京市城区地图上，太平南路的长度约为25cm，它的实际长度约为（）

A . 320cm B . 320m C . 2000cm D . 2000m

答案解析收藏纠错 + 选题
6. (2019九上·惠山期末) 如图，点A、B、C均在⊙O上，若∠ABC=40°，则∠AOC的大小是（）

A . 90° B . 80° C . 70° D . 50°

答案解析收藏纠错 + 选题
7. (2020九上·滦州期中)
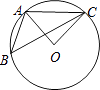
如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12m，由此他就知道了A、B间的距离．有关他这次探究活动的描述错误的是（　　）

A . AB=24m B . MN∥AB C . △CMN∽△CAB D . CM：MA=1：2

答案解析收藏纠错 + 选题
8. (2020·河南模拟) 如图，在矩形ABCD中，AB=3，BC=5，以B为圆心BC为半径画弧交AD于点E，连接CE，作BF⊥CE，垂足为F，则tan∠FBC的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2019九上·惠山期末) 若点M（﹣1，y₁），N（1，y₂），P（ $\text{[math]}$ ）都在抛物线y=﹣mx²+4mx+m²+1（m＞0）上，则下列结论正确的是（）

A . y₁＜y₂＜y₃ B . y₁＜y₃＜y₂ C . y₃＜y₁＜y₂ D . ₂＜y₁＜y₃

答案解析收藏纠错 + 选题
10. (2019九上·惠山期末) 在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A₁ ，作正方形A₁B₁C₁C；延长C₁B₁交x轴于点A₂ ，作正方形A₂B₂C₂C₁ ，按这样的规律进行下去，第2022个正方形（正方形ABCD看作第1个）的面积为（）

A . 5 $\text{[math]}$ （ $\text{[math]}$ ）²⁰²⁰ B . 5 $\text{[math]}$ （ $\text{[math]}$ ）²⁰²² C . 5 $\text{[math]}$ （ $\text{[math]}$ ）²⁰²¹ D . 5 $\text{[math]}$ （ $\text{[math]}$ ）²⁰²²

答案解析收藏纠错 + 选题

二、填空题

11. (2020·无锡模拟) 若 $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
12. (2019九上·惠山期末) 将函数y=﹣2x²的图象沿着x轴向右平移3个单位后所得到的图象的函数表达式为．

答案解析收藏纠错 + 选题
13. (2019九上·惠山期末) 14．已知关于x的一元二次方程（m-2）x²+2x+1=0有实数根，则m的取值范围是．

答案解析收藏纠错 + 选题
14. (2019九上·惠山期末) 如图，半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N，则劣弧弧MN的长度为．

答案解析收藏纠错 + 选题
15. (2019九上·惠山期末) 小红需要用扇形薄纸板制作成底面半径为9厘米，高为12厘米的圆锥形生日帽，如图所示，则该扇形薄纸板的圆心角为．

答案解析收藏纠错 + 选题
16. (2019九上·惠山期末) 如图，在△ABC中，∠ACB=90°，AB=9，cosB= $\text{[math]}$ ，把△ABC绕着点C旋转，使点B与AB边上的点D重合，点A落在点E，则点A、E之间的距离为.

答案解析收藏纠错 + 选题
17. (2019九上·惠山期末) 如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，D、E分别是AC、BC上的一点，且DE=3，若以DE为直径的圆与斜边AB相交于M、N，则MN的最大值为．

答案解析收藏纠错 + 选题

三、解答题

18. (2019九上·惠山期末) 解方程：
1. （1） x²－8x＋6＝0
2. （2） 2(x－1)²＝3x－3
答案解析收藏纠错 + 选题
19. (2019九上·惠山期末) 计算
1. （1） ﹣ $\text{[math]}$ +|1﹣4sin60°|；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2019九上·惠山期末) 如图，在边长为1的正方形网格中，有一格点△ABC，已知A、B、C三点的坐标分别是A（1，0）、B（2，－1）、C（3，1）．
1. （1） ①请在网格图形中画出平面直角坐标系；
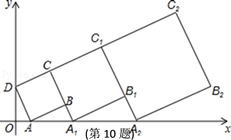
  ②以原点O为位似中心，将△ABC放大2倍，画出放大后的△A′B′C′；
  
  ③写出△A′B′C′各顶点的坐标，
2. （2）写出△A′B′C′的重心坐标.
答案解析收藏纠错 + 选题
21. (2019九上·惠山期末) 抚顺市某校想知道学生对“遥远的赫图阿拉”，“旗袍故里”等家乡旅游品牌的了解程度，随机抽取了部分学生进行问卷调查，问卷有四个选项（每位被调查的学生必选且只选一项）A．十分了解，B．了解较多，C．了解较少，D．不知道．将调查的结果绘制成如下两幅不完整的统计图，请根据两幅统计图中的信息回答下列问题：
1. （1）本次调查了多少名学生？
2. （2）补全条形统计图；
3. （3）该校共有500名学生，请你估计“十分了解”的学生有多少名？
4. （4）在被调查“十分了解”的学生中有四名学生会干部，他们中有3名男生和1名女生，学校想从这4人中任选两人做家乡旅游品牌宣传员，请用列表或画树状图法求出被选中的两人恰好是一男一女的概率．
答案解析收藏纠错 + 选题
22. 如图，为了测量建筑物AB的高度，在D处树立标杆CD，标杆的高是2m，在DB上选取观测点E、F，从E测得标杆和建筑物的顶部C、A的仰角分别为58°、45°．从F测得C、A的仰角分别为22°、70°．求建筑物AB的高度（精确到0.1m）．（参考数据：tan22°≈0.40，tan58°≈1.60，tan70°≈2.75．）

答案解析收藏纠错 + 选题
23. (2019九上·惠山期末) 如图，AB为⊙O的直径，C为⊙O上一点，∠CAB的角平分线AD交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E．
1. （1）求证：DE是⊙O的切线；
2. （2）若∠CAB=60°，DE=3 $\text{[math]}$ ，求AC的长．
答案解析收藏纠错 + 选题
24. (2019九上·武汉月考) “扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售量 $\text{[math]}$ （件）与销售单价 $\text{[math]}$ （元）之间存在一次函数关系，如图所示.
1. （1）求 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式；
2. （2）如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？
3. （3）该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围.
答案解析收藏纠错 + 选题
25. (2019九上·惠山期末) 如图，Rt△ABC中，∠C=90°，BC=8cm，AC=6cm．点P从B出发沿BA 向A运动，速度为每秒1cm，点E是点B以P为对称中心的对称点．点P运动的同时，点Q从A出发沿AC向C运动，速度为每秒2cm ．当点Q到达顶点C时，P，Q同时停止运动．设P， Q两点运动时间为t秒．
1. （1）当t为何值时，PQ∥BC ？
2. （2）设四边形PQCB的面积为y，求y关于t的函数解析式；
3. （3）四边形PQCB的面积与△APQ面积比能为3：2吗？若能，求出此时t的值；若不能，请说明理由；
4. （4）当t为何值时，△AEQ为等腰三角形？
答案解析收藏纠错 + 选题
26. (2019九上·惠山期末) 如图，在平面直角坐标系中，∠ACB＝90°，OC＝2BO，AC＝6，点B的坐标为（1，0），抛物线y＝﹣x²+bx+c经过A、B两点．
1. （1）求点A的坐标；
2. （2）求抛物线的解析式；
3. （3）点P是直线AB上方抛物线上的一点，过点P作PD垂直x轴于点D，交线段AB于点E，使PE＝ $\text{[math]}$ DE．
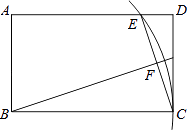
  ①求点P的坐标；
  
  ②在直线PD上是否存在点M，使△ABM为直角三角形？若存在，求出符合条件的所有点M的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
27. (2019九上·惠山期末) （发现问题）爱好数学的小明在做作业时碰到这样的一道题目：
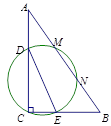
如图①，点O为坐标原点，⊙O的半径为1，点A（2，0）．动点B在⊙O上，连结AB，作等边△ABC（A，B，C为顺时针顺序），求OC的最大值

（解决问题）小明经过多次的尝试与探索，终于得到解题思路：在图①中，连接OB，以OB为边在OB的左侧作等边三角形BOE，连接AE．
1. （1）请你找出图中与OC相等的线段，并说明理由；
2. （2）求线段OC的最大值．
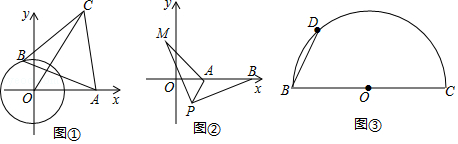
  （灵活运用）
3. （3）如图②，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA＝2，PM＝PB，∠BPM＝90°，求线段AM长的最大值及此时点P的坐标．
  （迁移拓展）
4. （4）如图③，BC＝4 $\text{[math]}$ ，点D是以BC为直径的半圆上不同于B、C的一个动点，以BD为边作等边△ABD，请直接写出AC的最值．
答案解析收藏纠错 + 选题