1. (2018九上·和平期末)       

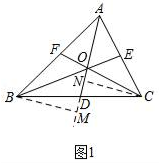
1. （1） 【探索发现】如图1，△ABC中，点D，E，F分别在边BC，AC，AB上，且AD，BE，CF相交于同一点O.用”S”表示三角形的面积，有S_△ABD：S_△ACD＝BD：CD，这一结论可通过以下推理得到：过点B作BM⊥AD，交AD延长线于点M，过点C作CN⊥AD于点N，可得S_△ABD：S_△ACD＝ ，又可证△BDM～△CDN，∴BM：CN＝BD：CD，∴S_△ABD：S_△ACD＝BD：CD.由此可得S_△BAO：S_△BCO＝；S_△CAO：S_△CBO＝；若D，E，F分别是BC，AC，AB的中点，则S_△BFO：S_△ABC＝.

   

3. （2） 【灵活运用】如图2，正方形ABCD中，点E，F分别在边AD，CD上，连接AF，BE和CE，AF分别交BE，CE于点G，M.

   

   若AE＝DF.判断AF与BE的位置关系与数量关系，并说明理由；

5. （3） 若点E，F分别是边AD，CD的中点，且AB＝4.则四边形EMFD的面积是多少？
7. （4） 【拓展应用】如图3，正方形ABCD中，AB＝4，对角线AC，BD相交于点O.点F是边CD的中点.AF与BD相交于点P，BG⊥AF于点G，连接OG，请直接写出S_△OGP的值.