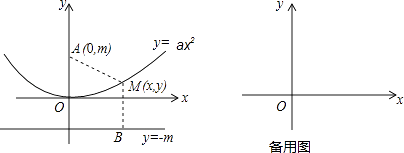1. (2015九上·宜春期末)

课题学习：我们知道二次函数的图象是抛物线，它也可以这样定义：如果一个动点M（x，y）到定点A（0，m）（m＞0）的距离与它到定直线y=﹣m的距离相等，那么动点M形成的图形就是抛物线y=ax²（a＞0）的图象，如图所示．

1. （1） 探究：当x≠0时，a与m有何数量关系？

3. （2） 应用：已知动点M（x，y）到定点A（0，4）的距离与到定直线y=﹣4的距离相等，请写出动点M形成的抛物线的解析式．

5. （3） 拓展：根据抛物线的平移变换，抛物线y= （x﹣1）²+2的图象可以看作到定点A（，）的距离与它到定直线y=的距离相等的动点M（x，y）所形成的图形．

7. （4） 若点D的坐标是（1，8），在（2）中求得的抛物线上是否存在点P，使得PA+PD最短？若存在，求出点P的坐标，若不存在，请说明理由．