1. (2017九上·宣化期末) 问题提出

平面内不在同一条直线上的三点确定一个面，那么平面内的四点（任意三点均不在同一直线上），能否在同一个面上呢？

初步思考

设不在同一条直线上的三点A、B、C确定的圆为⊙O．

1. （1） 当C、D在线段AB的同侧时．

   

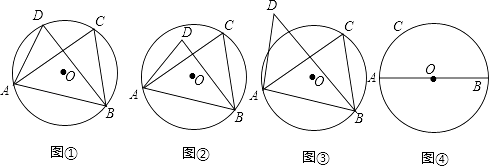
   如图①，若点D在⊙O上，此时有∠ACB=∠ADB，理由是．

   如图②，若点D在⊙O内，此时有∠ACB∠ADB；

   如图③，若点D在⊙O外，此时有∠ACB∠ADB（填“=”、“＞”、“＜”）

   由上面的探究，请直接写出A、B、C、D四点在同一个圆上的条件：．

   类比学习

3. （2） 仿照上面的探究思路，请探究：当C、D在线段AB的异侧时的情形．

   

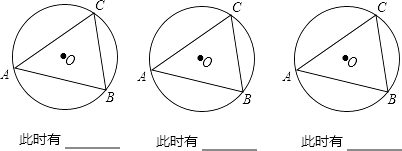
   由上面的探究，请用文字语言直接写出A、B、C、D四点在同一个圆上的条件：．

   拓展延伸

5. （3） 如何过圆上一点，仅用没有刻度的直尺，作出已知直径的垂线？

   已知：如图，AB是⊙O的直径，点C在⊙O上，求作：CN⊥AB

   作法：①连接CA、CB

   ②在CB上任取异于B、C的一点D，连接DA，DB；

   ③DA与CB相交于E点，延长AC、BD，交于F点；

   ④连接F、E并延长，交直径AB与M；

   ⑤连接D、M并延长，交⊙O于N，连接CN，则CN⊥AB．

   请安上述作法在图④中作图，并说明CN⊥AB的理由．（提示：可以利用（2）中的结论）