1. (2020八下·射阳期中) 我们已经知道(a﹣b)²≥0，即a²﹣2ab+b²≥0.所以a²+b²≥2ab(当且仅当a=b时取等号).

阅读1：若a、b为实数，且a＞0，b＞0.

∵( )²≥0，∴a﹣2 +b≥0，∴a+b≥2 (当且仅当a=b时取等号).

阅读2：若函数y=x (m＞0，x＞0，m为常数).由阅读1结论可知：x 即x ∴当x 即x²=m，∴x= (m＞0)时，函数y=x 的最小值为2 .

阅读理解上述内容，解答下列问题：

1. （1） 问题1：当x＞0时， 的最小值为；当x＜0时， 的最大值为.
3. （2） 问题2：函数y=a+ (a＞1)的最小值为.
5. （3） 问题3：求代数式 (m＞﹣2)的最小值，并求出此时的m的值.
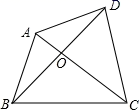
7. （4） 问题4：如图，四边形ABCD的对角线AC，BD相交于点O，△AOB、△COD的面积分别为4和16，求四边形ABCD面积的最小值.