1. (2017·济宁)

定义：点P是△ABC内部或边上的点（顶点除外），在△PAB，△PBC，△PCA中，若至少有一个三角形与△ABC相似，则称点P是△ABC的自相似点.

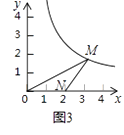
例如：如图1，点P在△ABC的内部，∠PBC=∠A，∠PCB=∠ABC，则△BCP∽△ABC，故点P是△ABC的自相似点.

请你运用所学知识，结合上述材料，解决下列问题：

在平面直角坐标系中，点M是曲线y= （x＞0）上的任意一点，点N是x轴正半轴上的任意一点.

1. （1）

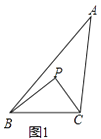
   如图2，点P是OM上一点，∠ONP=∠M，试说明点P是△MON的自相似点；当点M的坐标是（ ，3），点N的坐标是（ ，0）时，求点P的坐标；

   

3. （2）

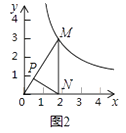
   如图3，当点M的坐标是（3， ），点N的坐标是（2，0）时，求△MON的自相似点的坐标；

   

5. （3） 是否存在点M和点N，使△MON无自相似点？若存在，请直接写出这两点的坐标；若不存在，请说明理由.