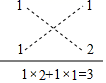1.
(2020八上·无为期末)
阅读材料:人教版八年级上册数学教材第121页的“阅读与思考”内容介绍,在因式分解中有一类形如x2+(p+q)x+pq的多项式,其常数项是两个因数的积,而一次项系数恰好是这两个因数的和,则我们可以把它分解成x2+(p+q)x+pq=(x+p)(x+q).
例如,x2+3x+2=x2+(1+2)x+1×2=(x+1)(x+2),具体做法是先分解二次项系数,分别写在十字交叉线的左上角和左下角,再分解常数项,分别写在十字交叉线的右上角和右下角:然后交叉相乘,求代数和,使其等于一次项系数(如图),这种方法称为“十字相乘法”.
解决问题:
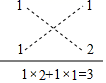
-
(1)
请模仿上例,运用十字相乘法将多项式x2﹣x﹣6因式分解(画出十字相乘图)
-
-
(2)
若多项式x2+kx﹣12可以分解成(x+m)(x+n)(m , n为整数)的形式,则m+n的最大值为.
-