安徽省芜湖市无为县2019-2020学年八年级上学期数学期末...

更新时间：2024-07-13 浏览次数：303 类型：期末考试

一、单选题

1. (2024八下·巴楚期中) 下列垃圾分类的图标（不含文字与字母部分）中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020八上·商城月考) 下列长度的三条线段中，能围成三角形的是（）

A . 5cm ， 6cm ， 12cm B . 3cm ， 4cm ， 5cm C . 4cm ， 6cm ， 10cm D . 3cm ， 4cm ， 8cm

答案解析收藏纠错 + 选题
3. (2020八上·无为期末) 下列运算正确的是（）

A . x²+x²＝2x⁴ B . （x+3y）（x﹣3y）＝x²﹣3y² C . a^﹣²•a³＝a D . （﹣2x²）⁴＝16x⁶

答案解析收藏纠错 + 选题
4. (2020八上·商城月考) 如图，AC与BD相交于点O ， ∠DAB＝∠CBA ，添加下列哪一个条件后，仍不能使△ADB≌△CBA的是（）

A . AD＝BC B . ∠ABD＝∠BAC C . OA＝OB D . AC＝BD

答案解析收藏纠错 + 选题
5. (2020八上·无为期末) 分式 $\text{[math]}$ 的值等于0，则a的值为（）

A . ±1 B . 1 C . ﹣1 D . 2

答案解析收藏纠错 + 选题
6. (2020八上·无为期末) 经过我省的合福高铁被称为“最美高铁”，从合肥途径无为至福州全程848km的路段，乘坐相谱号高速列车比乘坐普通列车全程直达所用时间缩短了5h ，已知高铁的平均时速是普通列车平均时速的2.5倍，若设普通列车的平均时速为xkm/h ．则根据题意可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020八上·无为期末) 如图，将图1中阴影部分拼成图2，根据两个图形中阴影部分的关系，可以验证下列哪个计算公式（）

A . （a﹣b）²＝a²﹣2ab+b² B . （a+b）²＝a²+2ab+b² C . （a﹣b）²＝（a+b）²﹣4ab D . （a+b）（a﹣b）＝a²﹣b²

答案解析收藏纠错 + 选题
8. (2022八上·南宁月考) 在4×4的正方形网格中，以格点为顶点的三角形称为格点三角形，在图中画出与△ABC关于某条直线对称的格点三角形，最多能画（）个．

A . 5 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题
9. (2020八上·无为期末) 如图，在△ABC中，∠BAC的平分线AD和边BC的垂直平分线ED相交于点D ，过点D作DF垂直于AC交AC的延长线于点F ，若AB＝8，AC＝5，则CF＝（）

A . 1.5 B . 2 C . 2.5 D . 3

答案解析收藏纠错 + 选题
10. (2020八上·无为期末) 若x≠1，则我们把﹣ $\text{[math]}$ 称为x的“和1负倒数”，如：2的“和1负倒数”为﹣ $\text{[math]}$ ，﹣3的“和1负倒数”为 $\text{[math]}$ ．若x₁＝ $\text{[math]}$ ，x₂是x₁的“和1负倒数”，x₃是x₂的“和1负倒数”，…，依此类推，则x₂₀₁₉的值为（）

A . $\text{[math]}$ B . ﹣ $\text{[math]}$ C . $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023八上·荣县月考) 纳米（nm）是非常小的长度单位，1nm＝10^﹣⁹m ．某种猪瘟病毒的直径为120nm ， “120nm”用科学记数法表示为m ．

答案解析收藏纠错 + 选题
12. (2023八上·新疆维吾尔自治区期末) 已知点A（a+2，5）与点B（5，b）关于x轴对称，则a﹣b＝．

答案解析收藏纠错 + 选题
13. (2023八上·新疆维吾尔自治区期末) 因式分解：2x³y﹣8xy＝．

答案解析收藏纠错 + 选题
14. (2020八上·无为期末) 如图，在一张直角三角形纸片ABC中，∠ACB＝90°，∠A＝30°P是边AB上的一动点，将△ACP沿着CP折叠至△A₁CP ，当△A₁CP与△ABC的重叠部分为等腰三角形时，则∠ACP的度数为．

答案解析收藏纠错 + 选题

三、解答题

15. (2021八上·巢湖期末) 计算：（﹣2x）²﹣（2x+1）（2x﹣1）+（x﹣2）²

答案解析收藏纠错 + 选题
16. (2020八上·无为期末) 解分式方程： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2020八上·无为期末) 先化简，再求值： $\text{[math]}$ ÷（a﹣ $\text{[math]}$ ），其中a＝3，b＝1．

答案解析收藏纠错 + 选题
18. (2020八上·无为期末) 阅读材料：人教版八年级上册数学教材第121页的“阅读与思考”内容介绍，在因式分解中有一类形如x²+（p+q）x+pq的多项式，其常数项是两个因数的积，而一次项系数恰好是这两个因数的和，则我们可以把它分解成x²+（p+q）x+pq＝（x+p）（x+q）．
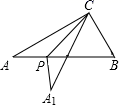
例如，x²+3x+2＝x²+（1+2）x+1×2＝（x+1）（x+2），具体做法是先分解二次项系数，分别写在十字交叉线的左上角和左下角，再分解常数项，分别写在十字交叉线的右上角和右下角：然后交叉相乘，求代数和，使其等于一次项系数（如图），这种方法称为“十字相乘法”．

解决问题：
1. （1）请模仿上例，运用十字相乘法将多项式x²﹣x﹣6因式分解（画出十字相乘图）
2. （2）若多项式x²+kx﹣12可以分解成（x+m）（x+n）（m ， n为整数）的形式，则m+n的最大值为．
答案解析收藏纠错 + 选题
19. (2020八上·无为期末) 如图，在平面直角坐标系中有一个△ABC，顶点A（﹣1，3），B（2，0），C（﹣3，﹣1）．
1. （1）画出△ABC关于y轴的对称轴图形△A₁B₁C₁（不写画法）；
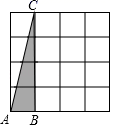
  点A₁的坐标为；点B₁的坐标为；点C₁的坐标为．
2. （2）若网格上的每个小正方形的边长为1，则△ABC的面积是．
答案解析收藏纠错 + 选题
20. (2020八上·无为期末) 如图，已知∠AOB ，以O为圆心，以任意长为半径作弧，分别交OA ， OB于F ， E两点，再分别以E ， F为圆心，大于 $\text{[math]}$ EF长为半径作圆弧，两条圆弧交于点P ，作射线OP ，过点F作FD∥OB交OP于点D.
1. （1）若∠OFD＝116°，求∠DOB的度数；
2. （2）若FM⊥OD ，垂足为M ，求证：△FMO≌△FMD.
答案解析收藏纠错 + 选题
21. (2020八上·无为期末) 为了响应习近平总书记“绿水青山就是金山银山”的号召，芜湖市对境内24km长江干流岸线环境进行集中专项整治，全部工程由甲乙两家施工队共同分别从上、下游同时进行，已知乙施工队的平均整治速度是甲施工队的1.5倍，原计划用若干天完成，后来为了提前完工，两家施工队都将施工速度提高20%，结果比原计划提前两天完成全部整治任务，求甲施工队原计划平均每天整治多少m？

答案解析收藏纠错 + 选题
22. (2020八上·无为期末) 已知a ， b是实数，定义关于“△”的一种运算如下：a△b＝（a﹣b）²﹣（a+b）² ．
1. （1）小明通过计算发现a△b＝﹣4ab ，请说明它成立的理由．
2. （2）利用以上信息得x $\text{[math]}$ ＝，若x $\text{[math]}$ ＝3，求（x $\text{[math]}$ ）⁴的值．
3. （3）请判断等式（a△b）△c＝a△（b△c）是否成立？并说明理由．
答案解析收藏纠错 + 选题
23. (2020八上·无为期末) 学习与探究：
在等边△ABC中，P是射线AB上的一点．
1. （1）探索实践：
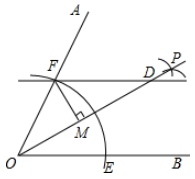
  如图1，P是边AB的中点，D是线段CP上的一个动点，以CD为边向右侧作等边△CDE ， DE与BC交于点M ，连结BE ．
  
  ①求证：AD＝BE；
  
  ②连结BD ，当DB+DM最小时，试在图2中确定D的位置，并说明理由；（要求用尺规作图，保留作图痕迹）
  
  ③在②的条件下，求△CME与△ACM的面积之比．
2. （2）思维拓展：
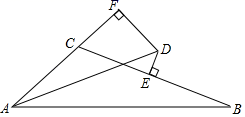
  如图3，点P在边AB的延长线上，连接CP ，点B关于直线CP的对称点为B'，连结AB'，CB'，AB'交BC于点N ，交直线CP于点G ，连结BG ．请判断∠AGC与∠AGB的大小关系，并证明你的结论．
答案解析收藏纠错 + 选题