1. (2017·青岛) 数和形是数学的两个主要研究对象，我们经常运用数形结合、数形转化的方法解决一些数学问题．下面我们来探究“由数思形，以形助数”的方法在解决代数问题中的应用．

1. （1）

   探究一：求不等式|x﹣1|＜2的解集

   探究|x﹣1|的几何意义

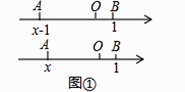
   如图①，在以O为原点的数轴上，设点A′对应的数是x﹣1，由绝对值的定义可知，点A′与点O的距离为|x﹣1|，可记为A′O=|x﹣1|．将线段A′O向右平移1个单位得到线段AB，此时点A对应的数是x，点B对应的数是1．因为AB=A′O，所以AB=|x﹣1|，因此，|x﹣1|的几何意义可以理解为数轴上x所对应的点A与1所对应的点B之间的距离AB．

   

   探究求方程|x﹣1|=2的解

   因为数轴上3和﹣1所对应的点与1所对应的点之间的距离都为2，所以方程的解为3，﹣1．

   探究：

   求不等式|x﹣1|＜2的解集

   因为|x﹣1|表示数轴上x所对应的点与1所对应的点之间的距离，所以求不等式解集就转化为求这个距离小于2的点对应的数x的范围．

   请在图②的数轴上表示|x﹣1|＜2的解集，并写出这个解集．

   

3. （2）

   探究二：探究 的几何意义

    

   探究：

   的几何意义

   如图③，在直角坐标系中，设点M的坐标为（x，y），过M作MP⊥x轴于P，作MQ⊥y轴于Q，则P点坐标为（x，0），Q点坐标为（0，y），OP=|x|，OQ=|y|，在Rt△OPM中，PM=OQ=|y|，则MO= = = ，因此，  的几何意义可以理解为点M（x，y）与点O（0，0）之间的距离MO．

   

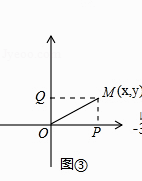
   探究：

   的几何意义

   如图④，在直角坐标系中，设点A′的坐标为（x﹣1，y﹣5），由探究二（1）可知，A′O= ，将线段A′O先向右平移1个单位，再向上平移5个单位，得到线段AB，此时点A的坐标为（x，y），点B的坐标为（1，5），因为AB=A′O，所以AB= ，因此 的几何意义可以理解为点A（x，y）与点B（1，5）之间的距离AB．

   

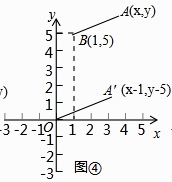
   探究 的几何意义

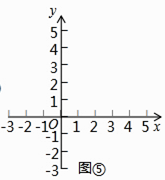
   ①请仿照探究二的方法，在图⑤中画出图形，并写出探究过程．

   ② 的几何意义可以理解为：

   

5. （3） 拓展应用：

   ① + 的几何意义可以理解为：点A（x，y）与点E（2，﹣1）的距离和点A（x，y）与点F（填写坐标）的距离之和．

   ② + 的最小值为（直接写出结果）