1. (2017·阜宁模拟)

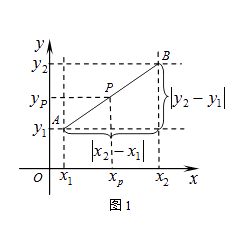
阅读材料：如图1，在平面直角坐标系中，A、B两点的坐标分别为A（x₁ ， y₁），B（x₂ ， y₂），AB中点P的坐标为（x_p ， y_p）．由x_p﹣x₁=x₂﹣x_p ， 得x_p= ，同理y_p= ，所以AB的中点坐标为（ ， ）．由勾股定理得AB²=|x₂﹣x₁|₂+|y₂﹣y₁|² ， 所以A、B两点间的距离公式为AB= ．这两公式对A、B在平面直角坐标系中其它位置也成立．解答下列问题：

1. （1） 已知M（1，﹣2），N（﹣1，2），直接利用公式填空：MN中点坐标为，MN=．

3. （2）

   如图2，直线l：y=2x+2与抛物线y=2x²交于A、B两点，P为AB的中点，过P作x轴的垂线交抛物线于点C．

   

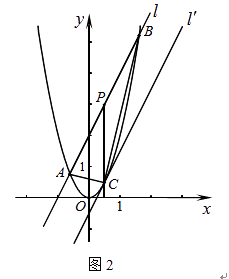
   （a）求A、B两点的坐标及C点的坐标；

   （b）连结AB、AC，求证△ABC为直角三角形；

   （c）将直线l平移到C点时得到直线l′，求两直线l与l′的距离．