1. (2017·东城模拟) 佳佳向探究一元三次方程x³+2x²﹣x﹣2=0的解的情况，根据以往的学习经验，他想到了方程与函数的关系，一次函数y=kx+b（k≠0）的图象与x轴交点的横坐标即为一元一次方程kx+b（k≠0）的解，二次函数y=ax²+bx+c（a≠0）的图象与x轴交点的横坐标即为一元二次方程ax²+bx+c=0（a≠0）的解，如：二次函数y=x²﹣2x﹣3的图象与x轴的交点为（﹣1，0）和（3，0），交点的横坐标﹣1和3即为x²﹣2x﹣3=0的解．

根据以上方程与函数的关系，如果我们直到函数y=x³+2x²﹣x﹣2的图象与x轴交点的横坐标，即可知方程x³+2x²﹣x﹣2=0的解．

佳佳为了解函数y=x³+2x²﹣x﹣2的图象，通过描点法画出函数的图象．

x

…

﹣3

﹣

﹣2

﹣

﹣1

﹣

0

1

2

…

y

…

﹣8

﹣

0

m

﹣

﹣2

﹣

0

12

…

1. （1） 直接写出m的值，并画出函数图象；
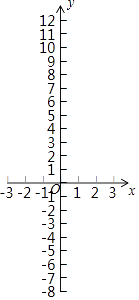
3. （2） 根据表格和图象可知，方程的解有个，分别为；
5. （3） 借助函数的图象，直接写出不等式x³+2x²＞x+2的解集．