1. (2020高二下·武汉期中) 某景区的各景点从2009年取消门票实行免费开放后，旅游的人数不断地增加，不仅带动了该市淡季的旅游，而且优化了旅游产业的结构，促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变．下表是从2009年至2018年，该景点的旅游人数 （万人）与年份 的数据：

第x年	1	2	3	4	5	6	7	8	9	10
旅游人数y（万人）	300	283	321	345	372	435	486	527	622	800

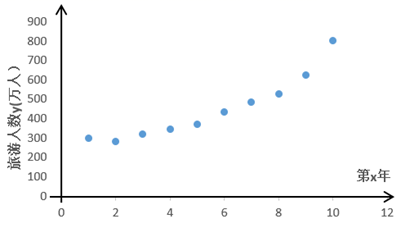
该景点为了预测2021年的旅游人数，建立了 与 的两个回归模型：

模型①：由最小二乘法公式求得 与 的线性回归方程 ；

模型②：由散点图的样本点分布，可以认为样本点集中在曲线 的附近．

参考公式、参考数据及说明：

①对于一组数据 ，其回归直线 的斜率和截距的最小二乘法估计分别为 ．②刻画回归效果的相关指数 ；③参考数据： ， ．

	449	6.05	83	4195	9.00

表中 ．

1. （1） 根据表中数据，求模型②的回归方程 ．（ 精确到个位， 精确到0.01）．
3. （2） 根据下列表中的数据，比较两种模型的相关指数 ，并选择拟合精度更高、更可靠的模型，预测2021年该景区的旅游人数（单位：万人，精确到个位）．

   回归方程	①	②
   	30407	14607