1. (2021七下·太原期末) 综合与实践：

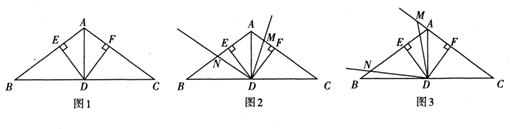
问题情境：如图1，在△ABC中，AB=AC，∠BAC为钝角，点D是BC的中点，DE⊥AB于点E，DF⊥AC于点F。试判断线段DE与DF的数量关系，并说明理由。

探究展示：小宇同学展示出如下正确的解法：

解：DE=DF，理由如下：

∵点D是BC的中点，∴AD是BC边上中线，

∵AB=AC，∴AD是∠BAC的角平分线(依据1)

∵DF⊥AC，DE⊥AB，∴DE=DF。(依据2)

1. （1） 反思交流：
   写出上述过程中的“依据1”和“依据2”：

   依据1：；

   依据2：。

3. （2） 请探究线段AE与AF的数量关系，并说明理由。
5. （3） 拓展延伸：
   请从下面A，B两题中任选一题作答。我选择题。

   A．在图1的条件下，点M是线段AF上一点，作∠MDN=∠EDF，射线DN交AB于点N，试判断AM+EN=AE是否成立，并说明理由。

   B．在图1的条件下，点M是线段FA延长上一点，作∠MDN=∠EDF，射线DN交线段BE于点N，试写出AM，EN与AE的等量关系并说明理由。