B . 
C . 
D . 
B . 
C . 
D . 
B . 沿AD折叠，点C落在AB边上的点E处 
C . 先沿DE折叠使点C与B重合，再沿AD折叠得到折痕AD 
D . 沿AD折叠，点C落在三角形外的点E处 
| x | …… | -1 | 0 | 1 | 2 | 3 | 4 | …… |
| y | …… | -2 | 0 | 2 | 4 | 6 | 8 | …… |
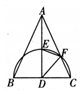
A．∠AFD=°(用含α的式子表示)
B．∠AFE=°
|
所处深度x( km) |
2 |
3 |
4 |
5 |
6 |
7 |
…… |
|
岩层的温度y(℃) |
90 |
125 |
195 |
265 |
…… |
“友好数对”
已知两个两位数，将它们各自的十位数字和个位数字交换位置后，得到两个与原两个两位数均不同的新数，若这两个两位数的乘积与交换位置后两个新两位数的乘积相等，则称这样的两个两位数为“友好数对”。例如：43×68=34×86=2924，所以43和68与34和86都是“友好数对”。
解：根据题意，“好友数对”中的两个数分别表示为10a+b和10c+d ，将它们各自的十位数字和个位数字交换位置后两个数依次表示为和
因为它们是友好数对，
所以(10a+b)(10c+d)=
即a，b，c，d的等量关系为：
A．请再写出一对“友好数对”，与本题已给的“友好数对”不同。
B．若有一个两位数，十位数字为x+2，个位数字为x，另一个两位数，十位数字为x+2，个位数字为x+8。且这两个数为“友好数对”，直接写出这两个两位数。
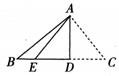
问题情境：如图1，在△ABC中，AB=AC，∠BAC为钝角，点D是BC的中点，DE⊥AB于点E，DF⊥AC于点F。试判断线段DE与DF的数量关系，并说明理由。
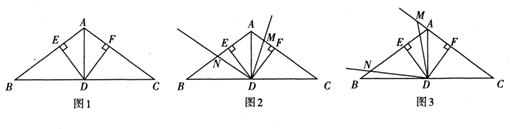
探究展示：小宇同学展示出如下正确的解法：
解：DE=DF，理由如下：
∵点D是BC的中点，∴AD是BC边上中线，
∵AB=AC，∴AD是∠BAC的角平分线(依据1)
∵DF⊥AC，DE⊥AB，∴DE=DF。(依据2)
依据1：；
依据2：。
A．在图1的条件下，点M是线段AF上一点，作∠MDN=∠EDF，射线DN交AB于点N，试判断AM+EN=AE是否成立，并说明理由。
B．在图1的条件下，点M是线段FA延长上一点，作∠MDN=∠EDF，射线DN交线段BE于点N，试写出AM，EN与AE的等量关系并说明理由。
