1. (2021九上·李沧月考) 几何模型：

条件：如图1，A、B是直线 同旁的两个定点．

问题：在直线 上确定一点P，使PA+PB的值最小．

方法：作点A关于直线 的对称点A′，连接A′B交 于点P，则PA+PB=A′B的值最小（不必证明）．

模型应用：

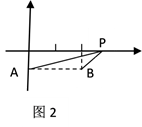
1. （1） 如图2，已知平面直角坐标系中两定点A（0，-1），B（2，-1），P为x轴上一动点， 则当PA+PB的值最小时，点P的横坐标是，此时PA+PB的最小值是；

   

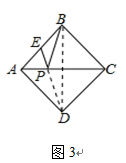
3. （2） 如图3，正方形ABCD的边长为2，E为AB的中点，P是AC上一动点.由正方形对称性可知，B与D关于直线AC对称，连接BD，则PB+PE的最小值是；

   

5. （3） 如图4，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一动点P，则PD＋PE的最小值为；

   

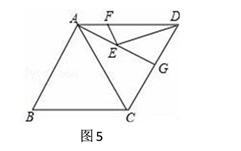
7. （4） 如图5，在菱形ABCD中，AB=8，∠B=60°，点G是边CD边的中点，点E、F分别是AG、AD上的两个动点，则EF+ED的最小值是.