山东省青岛市李沧区青岛爱迪学校2021-2022学年九年级上...

更新时间：2021-11-11 浏览次数：131 类型：月考试卷

一、单选题

1. (2021九上·青龙期中) 下列方程是一元二次方程的是（）

A . 2x²+y＝1 B . 9y＝3y﹣1 C . $\text{[math]}$ ﹣2x²＝8 D . 2x²＝1

答案解析收藏纠错 + 选题
2. (2023九上·京口期中) 根据表格中的信息，估计一元二次方程ax²+bx+c＝10（a、b、c为常数，a≠0）的一个解x的范围为（）

x

0

0.5

1

1.5

2

ax²+bx+c

﹣15

﹣8.75

﹣2

5.25

13

A . 0＜x＜0.5 B . 0.5＜x＜1 C . 1＜x＜1.5 D . 1.5＜x＜2

答案解析收藏纠错 + 选题
3. (2021九上·李沧月考) 如图，在矩形ABCD中，对角线AC与BD相交于点O，过点A作BD的垂线，垂足为E，已知∠EAB：∠EAD＝1：3，则∠EOA的度数为（）

A . 45° B . 40° C . 35° D . 30°

答案解析收藏纠错 + 选题
4. (2021九上·李沧月考) 青岛第四届海上马拉松比赛将在2020年11月举行，小明和小刚分别从A、B、C三个组中随机选择一个组参加志愿者活动，假设每人参加这三个组的可能性都相同，小明和小刚恰好选择同一组的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022八下·郧西月考) 菱形的两条对角线的长分别为 6cm、8cm，则菱形的边长是（）

A . 10cm B . 7cm C . 5cm D . 4cm

答案解析收藏纠错 + 选题
6. (2021九上·李沧月考) 如图，在△ABC中中，AD平分∠BAC，DE $\text{[math]}$ AC交AB于点E，DF $\text{[math]}$ AB交AC于点F，若AF＝8，则四边形AEDF的周长是（　　）

A . 24 B . 28 C . 32 D . 36

答案解析收藏纠错 + 选题
7. (2021九上·李沧月考) 如图，矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAD交BC于点E，∠CAE＝15°，则∠AOE的度数为（）

A . 120° B . 135° C . 145° D . 150°

答案解析收藏纠错 + 选题
8. (2022八下·普兰店期中) 如图，已知，矩形ABCD中，AB=3 cm，AD=9 cm，将此矩形折叠，使点B与点D重合，折痕为EF，则AE的长为（）

A . 3 cm B . 4 cm C . 5 cm D . $\text{[math]}$ cm

答案解析收藏纠错 + 选题

二、填空题

9. (2021九上·李沧月考) E为正方形ABCD的对角线AC上一点，且AE=AB，则∠EBC=．

答案解析收藏纠错 + 选题
10. (2021九上·李沧月考) 我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形．现有一个对角线分别为6cm和8cm的菱形，它的中点四边形的对角线长是．

答案解析收藏纠错 + 选题
11. (2021九上·李沧月考) 若一元二次方程 $\text{[math]}$ 有一根为 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2021九上·李沧月考) 书香相伴，香满校园，某校9月份借阅图书500本，11月份借阅图书845本，该校这两个月借阅图书的月均增长率是．

答案解析收藏纠错 + 选题
13. (2021九上·李沧月考) 如果（m²+n²﹣1）（m²+n²+2）＝4，则m²+n²＝．

答案解析收藏纠错 + 选题
14. (2022八下·侯马期末) 如图，在矩形ABCD中，AB＝3，AD＝4，P是AD上不与A和D重合的一个动点，过点P分别作AC和BD的垂线，垂足分别为E、F．求PE+PF＝．

答案解析收藏纠错 + 选题
15. (2021九上·李沧月考) 已知x₁ ， x₂是方程x²﹣4x+2＝0的两根，则
1. （1） $\text{[math]}$ 的值为；
2. （2） x₁²+x₂²的值为．
答案解析收藏纠错 + 选题
16. (2021九上·李沧月考) 如图，正方形 $\text{[math]}$ 的边长为4，点 $\text{[math]}$ 在 $\text{[math]}$ 上且 $\text{[math]}$ ， $\text{[math]}$ 为对角线 $\text{[math]}$ 上一动点，则 $\text{[math]}$ 周长的最小值为．

答案解析收藏纠错 + 选题

三、解答题

17. (2023九上·市南区期中) 小明想利用一块三角形纸片裁剪一个菱形，要求一个顶点为A，另外三个顶点分别在三角形的三边上，请你在原图上利用尺规作图把这个菱形作出来．

答案解析收藏纠错 + 选题
18. (2021九上·李沧月考) 解方程：
1. （1） x²+2x+2＝8x+4（配方法）．
2. （2） x²﹣7x﹣18＝0．
3. （3）（2x﹣3）²﹣2（2x﹣3）﹣3＝0．
答案解析收藏纠错 + 选题
19. (2021九上·李沧月考) 用如图所示的两个可以自由转动的转盘进行“配紫色”游戏：游戏者同时转动两个转盘，若其中一个转盘转出了红色，另一个转盘转出了蓝色，那么他就赢了．
1. （1）利用画树状图或列表的方法表示游戏所有可能出现的结果；
2. （2）求游戏者获胜的概率．
答案解析收藏纠错 + 选题
20. (2021九上·李沧月考) 已知：关于x的一元二次方程（k﹣1）x²+2x﹣1＝0有两个不相等的实数根．求：k的最小整数解．

答案解析收藏纠错 + 选题
21. (2021九上·李沧月考) 如图，菱形ABCD中，对角线AC、BD交于点O，AC=24，BD=10，DE⊥AB于E，
1. （1）求菱形ABCD的周长；
2. （2）求菱形ABCD的面积；
3. （3）求DE的长.
答案解析收藏纠错 + 选题
22. (2021九上·李沧月考) 尊老爱幼是中华民族的传统美德，九九重阳节前夕，某商店为老人推出一款特价商品，每件商品的进价为15元，促销前销售单价为25元，平均每天能售出80件；根据市场调查，销售单价每降低0.5元，平均每天可多售出20件.
1. （1）若每件商品降价5元，则商店每天的平均销量是件（直接填写结果）；
2. （2）不考虑其他因素的影响，若商店销售这款商品的利润要平均每天达到1280元，每件商品的定价应为多少元？（列方程求解）
答案解析收藏纠错 + 选题
23. (2021九上·李沧月考) 如图，在矩形ABCD中，AB＝20cm，动点P从点A开始沿AB边以4cm/s的速度运动，动点Q从点C开始沿CD边以1cm/s的速度运动．点P和点Q同时出发，当其中一点到达终点时，另一点也随之停止运动，设动点的运动时间为ts，则当t为何值时，四边形APQD是矩形？

答案解析收藏纠错 + 选题
24. (2021九上·李沧月考) 几何模型：
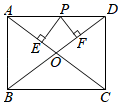
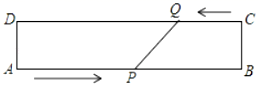
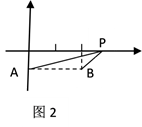
条件：如图1，A、B是直线 $\text{[math]}$ 同旁的两个定点．

问题：在直线 $\text{[math]}$ 上确定一点P，使PA+PB的值最小．

方法：作点A关于直线 $\text{[math]}$ 的对称点A′，连接A′B交 $\text{[math]}$ 于点P，则PA+PB=A′B的值最小（不必证明）．

模型应用：
1. （1）如图2，已知平面直角坐标系中两定点A（0，-1），B（2，-1），P为x轴上一动点，则当PA+PB的值最小时，点P的横坐标是，此时PA+PB的最小值是；
2. （2）如图3，正方形ABCD的边长为2，E为AB的中点，P是AC上一动点.由正方形对称性可知，B与D关于直线AC对称，连接BD，则PB+PE的最小值是；
3. （3）如图4，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一动点P，则PD＋PE的最小值为；
4. （4）如图5，在菱形ABCD中，AB=8，∠B=60°，点G是边CD边的中点，点E、F分别是AG、AD上的两个动点，则EF+ED的最小值是.
答案解析收藏纠错 + 选题