在由 个小正方形(边长为1)组成的矩形网格中,该矩形的一条对角线所穿过的小正方形个数与m,n有何关系?
(问题探究)
为探究规律,我们采用一般问题特殊化的策略,通过分类讨论,先从最简单的情形入手,再逐次递进,从中找出解决问题的方法.
当m,n互质(m,n除1外无其他公因数)时,观察图1并完成下表:
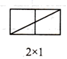
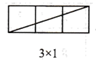
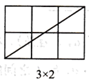
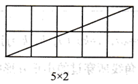
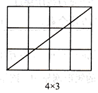
图1
| 矩形横长m | 2 | 3 | 3 | 5 | 4 | 5 | … |
| 公矩形纵长n | 1 | 1 | 2 | 2 | 3 | 3 | … |
| 矩形一条对角线所穿过的小正方形个数f | 2 | 3 | 4 | 6 | 6 |
| … |
结论:当m,n互质时,在 的矩形网格中,该矩形一条对角线所穿过的小正方形的个数f与m,n之间的关系式是.
当m,n不互质时,不妨设 ,
(a,b,k为正整数,且a,b互质),观察图2并完成下表:
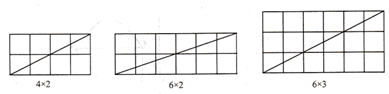
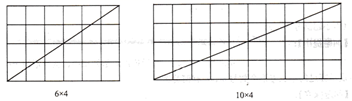
图2
| a | 2 | 3 | 3 | 5 | 2 | 3 | … |
| b | 1 | 1 | 2 | 2 | 1 | 1 | … |
| k | 2 | 2 | 2 | 2 |
| 3 | … |
| 矩形一条对角线所穿过的小正方形个数f | 4 | 6 | 8 |
| 6 |
| … |
结论:当m,n不互质时,若 ,
(a,b,k为正整数,且a,b互质).在
的矩形网格中,该矩形一条对角线所穿过的小正方形的个数f与a,b,k之间的关系式是.
一个由边长为1的小正方形组成的长为630,宽为490的矩形网格中,该矩形的一条对角线所穿过的小正方形个数是个.
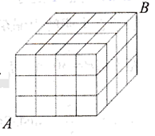
图3
如图3,在一个由48个棱长为1的小正方体组成的长方体中,经过顶点A,B的直线穿过的小正方体的个数是个.