



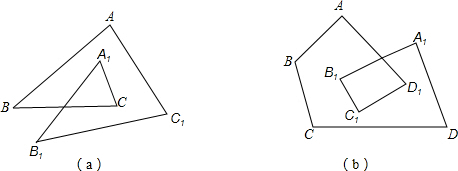

(关联运用)如图3,在等腰 和等腰
中,
,
在直线
上,
,连接
、
,则
的最小值是.



①设AM与NF的交点为点P.求证:AP=EF:
②若AB= , 则线段EF的长为
△CAB和△CDE都是直角三角形,∠ACB=∠DCE=90°,CB=mCA , CE=mCD , 连接AD , BE , 探究AD , BE的位置关系.
【问题探究】
操作:如图1,分别将半圆的圆心角
(
取1、4、5、10)所对的弧三等分(要求:仅用圆规作图,不写作法,保留作图痕迹);

交流:当时,可以仅用圆规将半圆
的圆心角
所对的弧三等分吗?
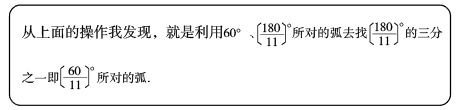
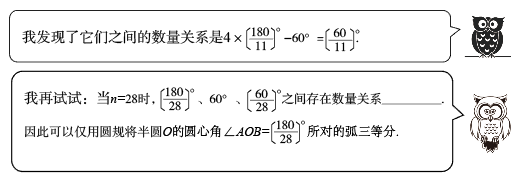
探究:你认为当满足什么条件时,就可以仅用圆规将半圆
的圆心角
所对的弧三等分?说说你的理由.


方法一:小敏利用刚学习的勾股定理进行解决,当 为等腰三角形时,
,设
,则
,所以
,在直角三角形ACD中,利用勾股定理可得,
,
解得 .故当
为等腰三角形时,CD的长为
.
方法二:小聪提前预习了函数这一章节的内容,他尝试利用函数的方法探究并解决该问题.
下面是他的探究讨程,请你补充完整.
|
CD |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
AD |
6 |
6.1 |
6.3 |
6.7 |
7.2 |
7.8 |
8.5 |
9.2 |
a |
①表格中 的值为.
②小聪分析得知不用测量BD的值,因为CD与BD满足关系式:.

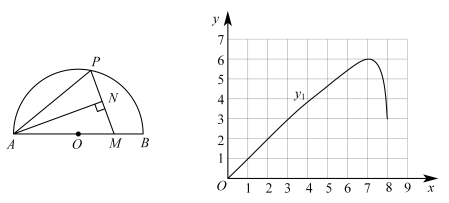
下面是小明的探究过程,请补充完整:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.64 | 7.78 | 7.90 | 8 |
| 0 | 0.99 | 1.99 | 2.97 | 3.92 | 4.82 | 5.61 | 5.90 | 5.56 | 5.18 | 4.46 | 3.30 | 0 |
| 6 | 5.91 | 5.65 | 5.21 | 4.53 | 3.56 | 2.12 | 0.24 | 2.25 | 3.01 | 4.0 | 5.00 | 6 |
请计算,当时,
;
①通过计算可知:;
②通过进一步探究函数图象可知:长度的近似值为
. (保留一位小数)
问题探究:

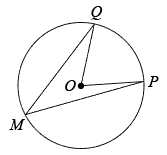
小明证明过程如下:
设直线交圆于点
, 连接
, 则
∵
∴
∴



当点A在线段BC上时,线段AC的长取得最小值,最小值为;
当点A在线段CB延长线上时,线段AC的长取得最大值,最大值为.
①证明: ;
②若 ,
,则线段BE长度的最大值为.

抛物线y=a(x-h)2+k(a>0)内有一定点F(h,),直线l过点M(h,
)且与x轴平行.当动点P在该抛物线上运动时,点P到直线l的距离PP1始终等于点P到点F的距离(该结论不需要证明).例如:抛物线y=2(x-1)2+3上的动点P到点F(1,
)的距离等于点P到直线l:y=
的距离.
请阅读上面的材料,探究下题:
如图4,点D(-1,)是第二象限内一定点,点P是抛物线y=
-1上一动点.当PO+PD取最小值时,请求出△POD的面积.
②如图2,若 , 将点P在
外部,求
之间数量关系(不需证明);
③如图3,写出之间的数量关系:(不需证明).

①写出图1中一个等于90°的角;
②图1中AF与DE的数量关系是.
问题情境:数学活动课上,王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质.
已知 , 点
为
上一动点,将
以
为对称轴翻折.同学们经过思考后进行如下探究:
独立思考:小明:“当点落在
上时,
. ”
小红:“若点为
中点,给出
与
的长,就可求出
的长.”
实践探究:奋进小组的同学们经过探究后提出问题1,请你回答:

问题1:在等腰中,
由
翻折得到.
问题解决:小明经过探究发现:若将问题1中的等腰三角形换成的等腰三角形,可以将问题进一步拓展.
问题2:如图3,在等腰中,
. 若
, 则求
的长.
在中,
,
, D是AB边上一点,且
(n为正整数),E是AC边上的动点,过点D作DE的垂线交直线BC于点F.

如图1,当时,兴趣小组探究得出结论:
, 请写出证明过程.
①如图2,当 , 且点F在线段BC上时,试探究线段AE,BF,AB之间的数量关系,请写出结论并证明;
②请通过类比、归纳、猜想,探究出线段AE,BF,AB之间数量关系的一般结论(直接写出结论,不必证明).
如图3,连接EF,设EF的中点为M. 若 , 求点E从点A运动到点C的过程中,点M运动的路径长(用含n的代数式表示).
婚礼上有116名宾客,地面上水平放置了一个长方体蛋糕,要保证这116名宾客都能分得蛋糕(忽略大小,水平切割的方向只能与地面平行,垂直切割只能与地面垂直),小明说我10刀即可完成任务,你认为小明是怎样切这个蛋糕才能完成任务.
问题探究:
为解决这个问题我们从最简单的长方形分割开始研究.
探究一:用一条直线分一个长方形,最多可以分成几部分?
如图1所示,一条线来分多出1部分,最多分成1+1=2部分;

探究二:用2条直线分一个长方形,最多可以分成几部分?
如图2所示,第2条线与第一条线相交,多出2部分,最多分成1+1+2=4部分;
探究三:用3条直线分一个长方形,最多可以分成几部分?
如图3所示,第3条线与前2条线相交,多出3部分,最多分成1+1+2+3=7部分;
探究四:用4条直线分一个长方形,最多可以分成几部分?
如图4所示,第4条线与原来3条线相交, 多出4部分,最多分1+1+2+3+4=11部分;
我们只需要在探究三的基础上,先在长方体中竖直切割3刀最多分成7块,平行于地面切一刀,此时4刀可切成7×2=14块.
探究八:如何用最少的切割次数,将一个长方体蛋糕切割成44块,请说明切割过程,无需画图;
问题解决:

数轴是一个非常重要的数学工具,它使数和数轴上的点建立起一一对应的关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.小明在一条长方形纸带上画了一条数轴,进行如下操作探究:
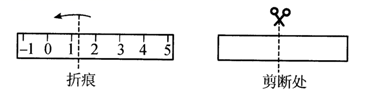


①当矩形是正方形时,
是 ▲ 三角形;
②当是等腰直角三角形时,求边
与边
之间的数量关系;
③若点P、、C共线,求证:
.


在由 个小正方形(边长为1)组成的矩形网格中,该矩形的一条对角线所穿过的小正方形个数与m,n有何关系?
(问题探究)
为探究规律,我们采用一般问题特殊化的策略,通过分类讨论,先从最简单的情形入手,再逐次递进,从中找出解决问题的方法.
当m,n互质(m,n除1外无其他公因数)时,观察图1并完成下表:
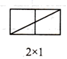
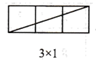
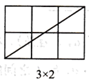
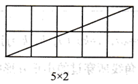
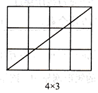
图1
| 矩形横长m | 2 | 3 | 3 | 5 | 4 | 5 | … |
| 公矩形纵长n | 1 | 1 | 2 | 2 | 3 | 3 | … |
| 矩形一条对角线所穿过的小正方形个数f | 2 | 3 | 4 | 6 | 6 |
| … |
结论:当m,n互质时,在 的矩形网格中,该矩形一条对角线所穿过的小正方形的个数f与m,n之间的关系式是.
当m,n不互质时,不妨设 ,
(a,b,k为正整数,且a,b互质),观察图2并完成下表:
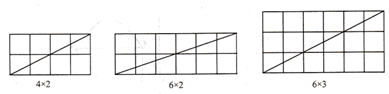
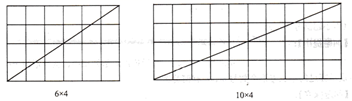
图2
| a | 2 | 3 | 3 | 5 | 2 | 3 | … |
| b | 1 | 1 | 2 | 2 | 1 | 1 | … |
| k | 2 | 2 | 2 | 2 |
| 3 | … |
| 矩形一条对角线所穿过的小正方形个数f | 4 | 6 | 8 |
| 6 |
| … |
结论:当m,n不互质时,若 ,
(a,b,k为正整数,且a,b互质).在
的矩形网格中,该矩形一条对角线所穿过的小正方形的个数f与a,b,k之间的关系式是.
一个由边长为1的小正方形组成的长为630,宽为490的矩形网格中,该矩形的一条对角线所穿过的小正方形个数是个.
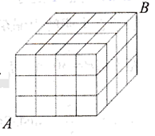
图3
如图3,在一个由48个棱长为1的小正方体组成的长方体中,经过顶点A,B的直线穿过的小正方体的个数是个.